数字（量的変数）の切り口【足し算の分解②】

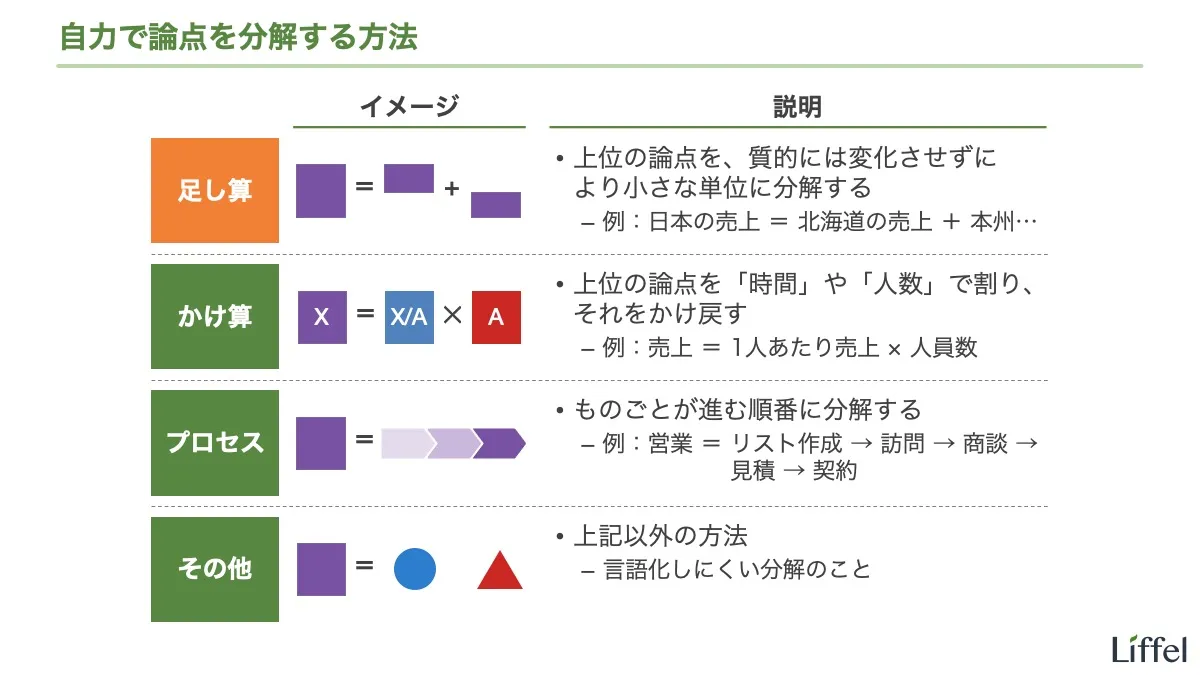
このエントリーでは、足し算の分解の切り口のうち、数字（量的変数）による分解を勉強しましょう。

なお、このエントリーは一連の「足し算の分解」の一部です。途中で分からなくなった場合は、以下のエントリーから順に読んでください。

では始めましょう。

toc

• 足し算の切り口①：数字
  • 分解の具体例
  • 練習問題
• 数字の切り口の注意点：階級を決める
  • 時間の単位（階級）
  • 練習問題
• 階級の決め方
  • ポイント①：階級は網羅的（MECE）にする
  • ポイント②：階級の幅
  • ポイント③：階級の数
    • 上限の階級の扱い
• 参考文献

足し算の切り口①：数字

足し算の分解の1つめの切り口は、数字です。表の上側ですね。専門用語では量的変数と呼ぶので、これも頭の片隅に置いておいてください。具体的には、以下のような切り口です。

• 時間
• 年齢
• 金銭
  • 収入
  • 価格
  • その他（売上、利益、コストなど）
• 重さ
• 速さ

これらはどれも、数字で表現できますよね。数字を切り口に分解するとは、これらの概念で論点を分解することです。

分解の具体例

具体例を見ていきましょう。ここでは、「どのような人が、この商品を買っているのか？」という論点を、2パターンの切り口で分解してみます。

まずは、年齢（年代）で分解してみましょう。以下のようになります。

• どのような人が、この商品を買っているのか？
  • 10歳未満（0歳代）の人か？
    • ※この年代が重要でない商品なら、落としてもOK
  • 10代の人か？
  • 20代の人か？
  • 30代の人か？
  • 40代の人か？
  • 50代の人か？
  • 60代以上の人か？

分解した論点に数字が含まれていることを確認してください。

次は、同じ論点を収入で分解してみましょう。

• どのような人が、この商品を買っているのか？
  • 年収200万円未満の人か？（x < 200）
  • 年収200万〜400万円の人か？（200≦ x < 400）
  • 年収400万〜600万円の人か？（400≦ x < 600）
  • 年収600万〜800万円の人か？（600≦ x < 800）
  • 年収800万〜1,000万円の人か？（800≦ x < 1000）
  • 年収1,000万円以上の人か？（1000 ≦ x）

同じように、分解した論点に数字が含まれますよね。このような分解が、数字を切り口にした論点の分解です。

練習問題

ここまでの内容を、練習問題で確認しましょう。

以下に解答欄があるので、答えを書いてみてください。

数字の切り口の注意点：階級を決める

数字の切り口で分解するときには、自分で適当な階級を設定する必要があります。階級とは、「数字の切り口で分解する際の区間」のことです。

先ほどの例で確認してみましょう。

• どのような人が、この商品を買っているのか？
  • 年収200万円未満の人か？（x < 200）
  • 年収200万〜400万円の人か？（200≦ x < 400）
  • 年収400万〜600万円の人か？（400≦ x < 600）
  • 年収600万〜800万円の人か？（600≦ x < 800）
  • 年収800万〜1,000万円の人か？（800≦ x < 1000）
  • 年収1,000万円以上の人か？（1000 ≦ x）

見てのとおり、この例では「200万円ごと」を階級にしています。言い換えると、200万円ごとの年収帯を作っているわけです。

数字で分解するときには、階級を必ず決めなければなりません。理由はシンプルで、階級を作らないと分解できないからです。

そもそも、「1円」や「1歳」レベルの間隔のデータは存在しないことも多い上に、それでは情報が分かりやすいレベルに収まりません。分解は目的ではなく上位の論点に答えるための手段なので、答えが出しやすいようにデータをまとめる必要があるのです。

時間の単位（階級）

なお、「時間」を切り口にする場合は、すでに細かい階級が専用の単位として用意されています。それだけ、時間は私たちの生活に深く根付いているということなのでしょう。

細かい話ですが、時間を切り口にする場合は、時点（いつなのか）と経過時間（ある時点から、どれだけ時間が経ったか）を区別してください。どちらも切り口として機能しますが、ゴチャゴチャになるのは避けましょう。ビジネスでよく使うのは時点の方です。

代表的な時間の単位を、以下にまとめました。状況に応じて、適切な大きさの単位を選んでください。

まずは時点の単位です。

• 時刻
  • 午前7時、8時、9時、、、
• 朝・昼・夜
  • ラフに分解したいときに便利
  • ただし、「朝（7時-12時）」のように、定義を明確にする
• 月（1月、2月、3月、、、）
• 四半期（3ヶ月ごと）
  • ビジネスでよく使う
• 年
• 数年間ごと
  • 例：2001-2005年、2006-2010年、2011-2015年、2016-2020年（5年間ごと）
• 数年おき
  • 例：2000年、2005年、2010年、2015年、2020年（5年おき）
  • 各年のデータが取れない場合か、超長期にわたって（50年間など）大雑把な傾向が見たいときのみ使う
    • 原則としては、データを隠すべきではない

次に、経過時間の単位です。

• 秒
• 分（60秒）
• 時間（60分）
• 日（24時間）
• 週（7日）
• 月
  • ただし、経過時間として「月」を使うと、それが何日間なのか曖昧になるので、「30日」などにしておいたほうが安全
• 年（365日）

必要に応じて、もっと細かい単位や、長い単位も使用してください。

練習問題

階級の決め方

では、どのように階級を決めたらよいのでしょう？　先ほどの例を再掲します。

• どのような人が、この商品を買っているのか？
  • 年収200万円未満の人か？（x < 200）
  • 年収200万〜400万円の人か？（200≦ x < 400）
  • 年収400万〜600万円の人か？（400≦ x < 600）
  • 年収600万〜800万円の人か？（600≦ x < 800）
  • 年収800万〜1,000万円の人か？（800≦ x < 1000）
  • 年収1,000万円以上の人か？（1000 ≦ x）

ポイントは以下の3つです。

1. 網羅的（MECE）にする
2. 階級の幅：できるだけ等間隔で階級を分ける
3. 階級の数：階級の数を分かりやすい範囲に収める

順に説明します。

ポイント①：階級は網羅的（MECE）にする

まず、階級は網羅的であるように（MECEであるように）設定します。わざわざ抜け漏れを作る理由がありません。上の例でも、年収が0円の人から無限大の人まで網羅されていますよね。

この際、言葉（自然言語）ではどうしてもダブりがないこと（互いに素であること）を表現しにくいので、分解の際には数式を意識するのがオススメです¹。

なお、網羅的に分解したあとで、明らかに重要でない階級を分析対象としない措置をすることは問題ありません。

ポイント②：階級の幅

次に、理由がないかぎり、階級の幅は等間隔にします。間隔の幅が都合よく変わっていては、階級ごとの比較ができないからです。例を確認しましょう。

• どのような人が、この商品を買っているのか？
  • 年収200万円未満の人か？（x < 200）
  • 年収200万〜400万円の人か？（200≦ x < 400）
  • 年収400万〜600万円の人か？（400≦ x < 600）
  • 年収600万〜800万円の人か？（600≦ x < 800）
  • 年収800万〜1,000万円の人か？（800≦ x < 1000）
  • 年収1,000万円以上の人か？（1000 ≦ x）

この例では、上限以外は「200万円」の等間隔になっていますよね。なお、数字には「上限がない」という性質があるので、上限の階級だけは「XX以上」と扱うしかありません。

ただし、このルールは「何が何でも等間隔にする」というほど絶対的なわけではありません。年収だと、以下のように分解するパターンもよく見かけます。

• どのような人が、この商品を買っているのか？
  • 年収200万円未満の人か？（x < 200）
  • 年収200万〜400万円の人か？（200≦ x < 400）
  • 年収400万〜600万円の人か？（400≦ x < 600）
  • 年収600万〜800万円の人か？（600≦ x < 800）
  • 年収800万〜1,000万円の人か？（800≦ x < 1000）
  • 年収1,000万〜1,500万円の人か？（1000≦ x < 1500）
  • 年収1,500万〜2,000万円の人か？（1500≦ x < 2000）
  • 年収2,000万円以上の人か？（2000 ≦ x）

このケースだと、太字にした2つの階級の間隔は「500万円」で、それまでと同じ「200万円」ではありません。こうなる理由は、この年収帯の人を「200万円」で括ると、データの出現頻度が少なくなりすぎるからです。

これは階級の幅が途中で変わっていますが、もし1,000万〜2,000万の階級をきちんと分析したいなら、「1,000万円以上」と1つの階級にしてしまうよりは、こちらの分解をすべきですよね。

このように、階級の幅は、分析の目的と、データの出現頻度との兼ね合いで決めてください。

ポイント③：階級の数

最後に階級の数ですが、これに関する明確な答えは出せません。「最適な階級の数はいくつか？」という問いは、幾人もの研究者が検討したうえで、まだ決着のついていない問いのようです（参考）。

ただ、間違いなく言えるのは「階級が多すぎると分かりにくい」ということです。細かくすればよいわけではありません。

では、いくつくらいから分かりにくいのでしょう？　個人的には、8-9つあたりが限界かなと思います。それを超えるようなら、階級の幅を広げて数を減らすことを検討してもよいでしょう。

上限の階級の扱い

階級の幅と数を決めるうえでは、上限の階級には重要性が残らないようにするのが原則です。上側が無限大に広がっている以上、「その階級が重要だ」という話にはしたくないですからね。

目安としては、上限の階級におけるデータの出現頻度（度数）が10%以下になるとよいでしょう。これなら大事には見えません。逆に、10%を超えてくると、もう少し階級を細かくしたほうがよい気がします。

ということで、階級の幅と数に関してはハッキリしたことは言いにくいのですが、分析の目的やデータの出現頻度を見ながら、うまく調整してください。

以上、数字を切り口にした足し算の分解を説明しました。次回はカテゴリー（質的変数）を切り口にした分解を学びましょう。

また、ロジカルシンキング関連のエントリーは以下のページにまとめてあります。こちらも参考にしてください。

参考文献

Footnotes

1. もちろん、「未満」、「以上」などの言葉を厳密に運用すれば言葉でもダブりがないことを表現可能です。 ↩