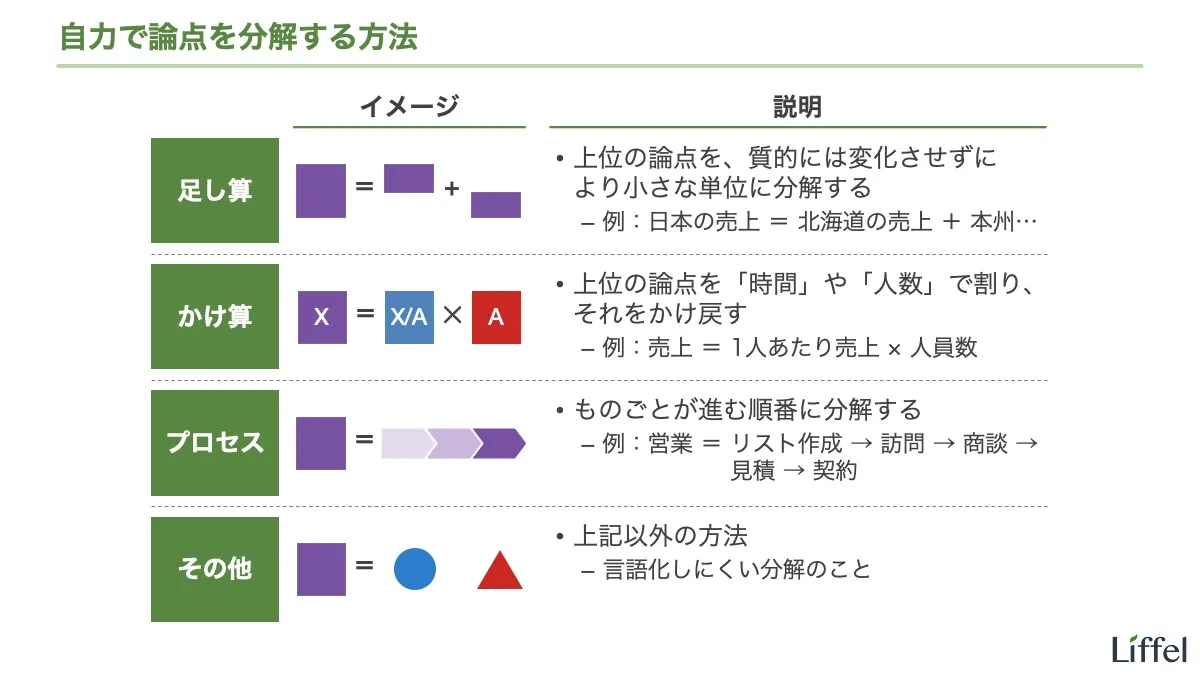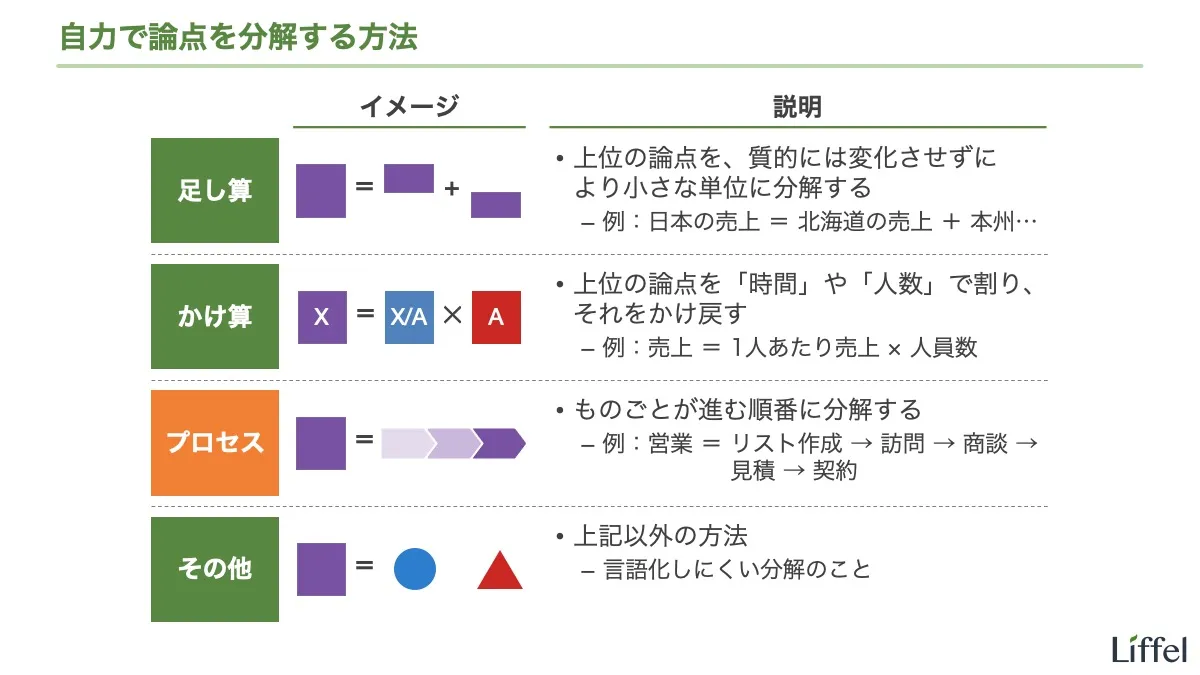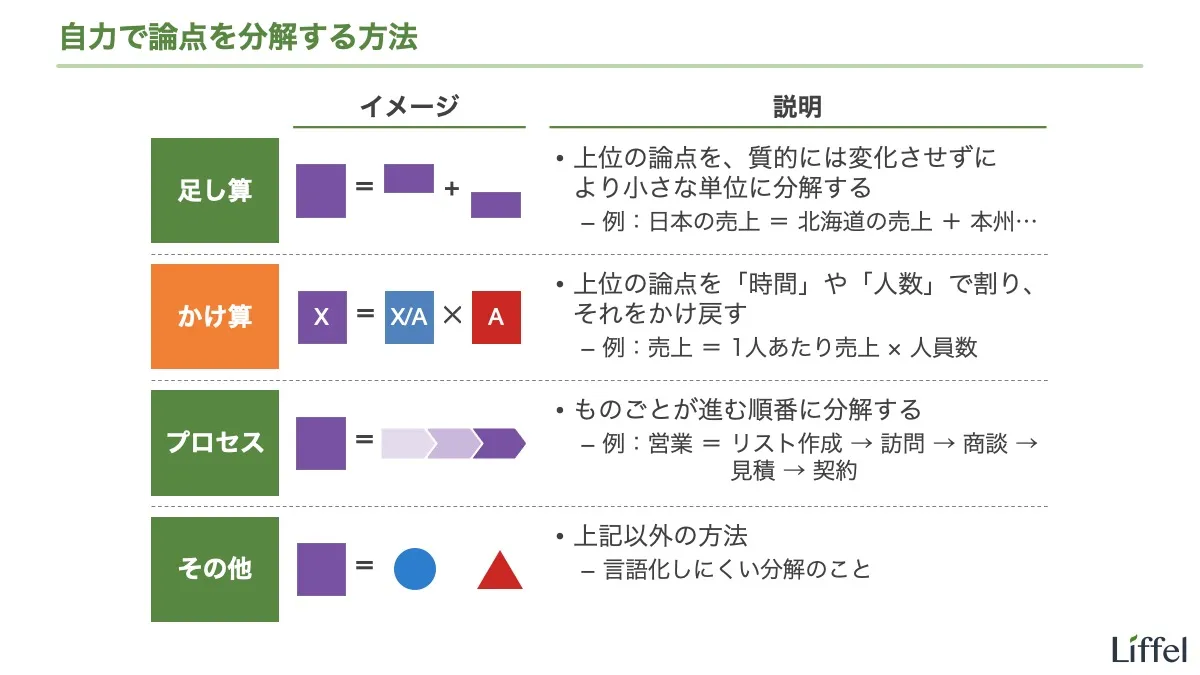
このエントリーでは、かけ算による論点の分解を勉強しましょう。足し算の分解に続いて、これもあらゆるシーンで使う基本的な分解です。
なお、このエントリーを読む前に、以下のエントリーを読んでおいてください。自力で論点を分解する方法の全体像を解説しています。
では始めましょう。
toc
かけ算の分解とは

かけ算の分解とは、ある要素で割ってから、その要素を掛け戻す分解です。
ある要素で割ってから、その要素を掛け戻す分解
まずは具体例を見てください。
- 日本のGDPを増やすには、どうすればよいか?
- 一人あたりGDP(国民の生産性)を増やすには、どうすればよいか?
- 日本人口を増やすには、どうすればよいか?
この分解では、「GDP」という概念を「人口」で割ってから、「人口」を掛け戻しています。「一人当たりGDP」とは、「GDP/人口」のことですからね。
抽象的に述べると、「Xという概念をAで割ってから、Aを掛け戻している」ということです。数式で表すと以下になります。
X = X/A × A
このような分解が、かけ算の分解です。
かけ算の分解は、正しく行えば数学的にイコールであることが担保されます。つまり、かけ算の分解は確実に網羅的(MECE)になります。足し算のように「その他」も出ないので、安心して使いやすいテクニックです。
かけ算の切り口
かけ算の切り口(上記の数式のAに該当するモノ)は、数字で表せる概念になります。数学的に処理するので、数字で表せない概念は使えません。
主に使われる切り口は、以下の2つです。この2つは必ず覚えてください。
- 時間
- 「1時間あたり」、「1日あたり」など
- 人間/集団の数
- 「一人あたり」、「チームあたり」、「店舗あたり」など
もちろん、数字になる概念であれば何でもOKなので、必要に応じて「個数」、「価格」、「重さ」なども使ってください。
練習問題
ここまでの内容を、練習問題で確認しましょう。
以下の論点を、かけ算で分解せよ。カッコ内に指定された切り口を使うこと。
どうしたら、バイトの収入を増やせるか?(時間)
以下に解答欄があるので、答えを書いてみてください。
- どうしたらバイトの収入を増やせるか?
- どうしたら時給を上げられるか?
- ※多くの場合、現在のバイトの時給を上げるのは現実的ではないので、「もっと時給のいいバイトを探す」という解決策になる
- どうしたらバイトをする時間を増やせるか?
- ※ここはさらに、「自分がバイトにあてられる時間」と、「シフトが空いている(労働可能な)時間」の両面から検討する必要がある
- どうしたら時給を上げられるか?
これは私が大学生のときに、実際に頭を悩ませた論点です。バイト収入を増やしたくても、この2つを同時に大きくすることは難しいんですよね。たとえば、家庭教師のような時給のいいバイトは時間量が稼げず、トータルの月収が大きくなりません。
今になって考えると、そもそもこんな論点を必死に考えていた時点で、大学生として何かを間違えていた可能性が高いのですが……。論点設定のミスというやつですね。
あなたは全国で募金活動をしている団体の幹部である。どうしたら、募金額を増やせるか?(人数)
- どうしたら、募金額を増やせるか?
- どうしたら、一人あたり募金額を増やせるか?
- どうしたら、募金してくれる人を増やせるか?
一人あたりの募金額を増やすのは、チャレンジングな論点ですね。どんな方法があるか、考えてみてください。
足し算の分解とかけ算の分解の違い
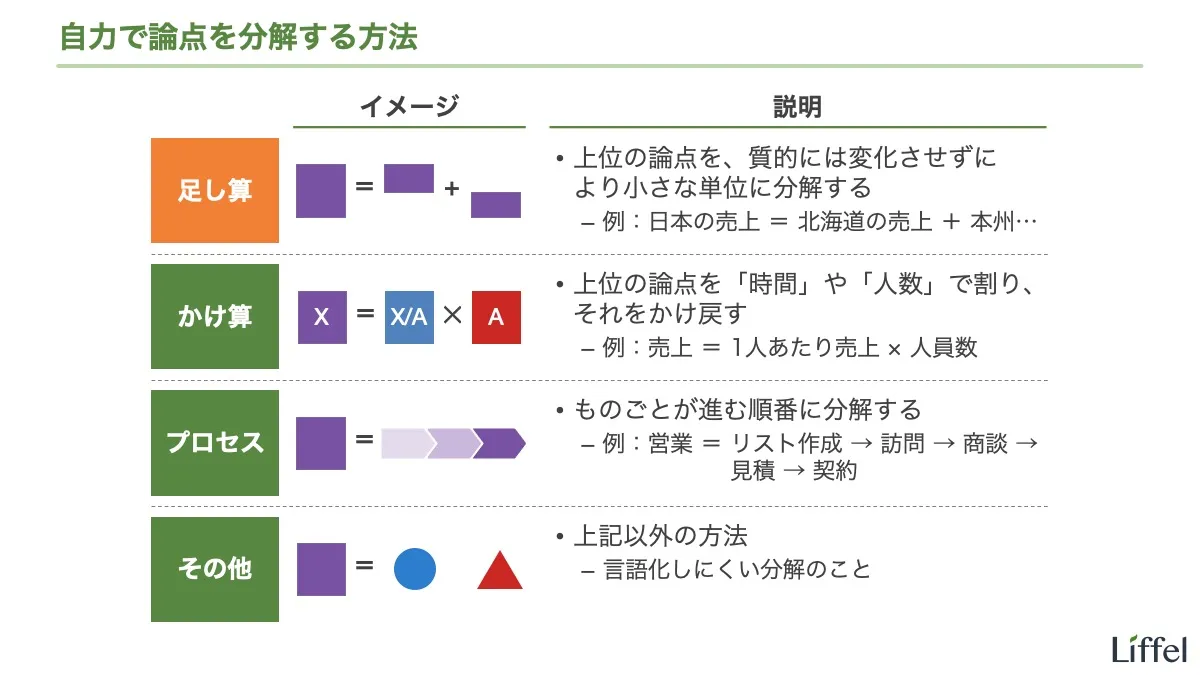
足し算の分解とかけ算の分解はセットで使うことも多いので、ここでそれぞれの特徴を整理します。
例として、先ほどの練習問題の「どうしたら、募金額を増やせるか?」という論点を使います。問題にも書いたとおり、前提として「日本中で募金活動をしている」ことにするので覚えておいてください。
足し算で分解してみる
まず、この論点を足し算で分解してみましょう。切り口は「地域」とします。結果は以下になります。
- どうしたら、(日本全国の)募金額を増やせるか?
- どうしたら、北海道の募金額を増やせるか?
- どうしたら、本州の募金額を増やせるか?
- どうしたら、四国の募金額を増やせるか?
- どうしたら、九州の募金額を増やせるか?
- どうしたら、沖縄の募金額を増やせるか?
これは足し算の分解なので、上位の論点と下位の論点で、論点の質が変化していないことを確認してください。共に、「募金額」という概念を扱っていますよね。
ここに足し算の分解の弱点があります。足し算の分解では概念が変化しないため、どれだけ足し算で分解しても、解決策を考えるヒントは出てきません。
分解を見れば明らかなとおり、この分解では「考えることの対象範囲」が小さくなっているだけで、「考えること(どうすれば、募金額を増やせるか?)」自体は変化していません。よって、この分解では、論点を分解しても解決策が考えやすくなるようなヒントは得られないわけです。
足し算の分解は概念が変化しないので、解決策を考えるヒントにはならない
この説明だけではピンとこないでしょう。かけ算の分解と比較してみましょう。
かけ算で分解してみる
では、同じ論点をかけ算で分解した例を見てみましょう。先ほどの解答例のとおりです。
- どうしたら、募金額を増やせるか?
- どうしたら、一人あたり募金額を増やせるか?
- どうしたら、募金してくれる人を増やせるか?
この分解では、「募金額」という概念が「一人あたり募金額」と「募金者の数」という、質的に異なる概念に変化しています。
そして、この分解は考えるヒントになりますよね。たとえば、「一人あたり募金額」にテコ入れするなら、以下のようなアイデアがすぐに出てくるでしょう。
- 募金時に「たくさんお願いします!」と一声かける
- 一定額以上の募金にはお礼を渡す
- 金持ちが多そうな地域を狙う
なお、どれもアイデアなので、実現性は考えないでください。
一方、「募金者の数」をどうにかするなら、以下のようなアイデアが考えられます。
- 大々的に宣伝をする
- メンバー(募金を募る人)の格好を派手にする/外見が魅力的な人を使う
- 人が多い地域を狙う
ここで押さえてほしいのは、ある概念を違う概念に変換したから、このようなアイデアが生まれやすくなっているということです。
この例では、「募金額」という概念を「一人あたり募金額」と「募金者の数」という、質的に異なる概念に変換したことによって、それがヒントになってアイデアが生まれているのです。もちろん、「募金額」のままでもアイデアを出せますが、「一人あたり募金額」と「募金者の数」の2つを別々に考えたほうが、具体的で多様なアイデアが出ます。これが「考えるヒントになる」ということです。
かけ算の分解は概念が変化するので、解決策を考えるヒントになる
使い分けの方針
では、足し算の分解には優位性がなく、常にかけ算の分解を使うべきなのでしょうか? もちろん、そんなことはありません。
実は、先ほどの足し算の分解はスマートとは言えません。欠点を強調するため、わざと下手にやりました。以下のように分解したほうが、足し算の分解の強みを発揮できます。
- どうしたら、(日本全国の)募金額を増やせるか?
- どこの地域に注力するべきか?
- 北海道か?
- 本州か?
- 四国か?
- 九州か?
- 沖縄か?
- (注力すべき地域において)どのように募金額を増やすべきか?
- どうしたら、一人あたり募金額を増やせるか?
- どうしたら、募金してくれる人を増やせるか?
- どこの地域に注力するべきか?
このように、まずは「注力すべき地域」を特定するのに足し算の分解を使うと、先ほどと違い、足し算の分解にも意味が生まれますよね。その後にかけ算の分解を使って、具体的な行動を考えるわけです。
このように考えると、日本全国を平たくアプローチするより効率的にリソースを使えそうです。
足し算の分解の使い道
このように、足し算の分解は「重要度の大きい部分」を見つけるのに役立ちます。上の例のように「地域」で分解すれば「重要な地域」がわかるし、「時間」で分解すれば「重要なタイミング」がわかります。
「重要なところに集中する」というのは、当たり前すぎて安っぽく聞こえるかもしれませんが、大事なことです。足し算の分解はそれを考えるのに役立ちます。
足し算の分解は「重要度の大きい部分」を見つけるために使う。
逆に言うと、足し算の分解でわかるのはそこまでです。大事そうなところにアタリをつけたら、そこから先は足し算の分解は役に立ちません。かけ算の分解や、この後に紹介するプロセスの分解といった、ほかの分解を使う必要があります。
オススメの基本パターンは、足し算 → かけ算と分解してみることです。足し算で「どこ」にアタリをつけて、かけ算で「なぜ/どうしたら」に切り込む。これが基本のワンツーパンチなので、初心者の人はこの型を意識してみてください。
以上、かけ算の分解を説明しました。次はプロセスの分解を勉強しましょう。
また、ロジカルシンキング関連のエントリーは以下のページにまとめてあります。こちらも参考にしてください。