このエントリーでは、根拠の普遍性について学びましょう。妥当な根拠を構築するうえで、とても重要な条件です。また、最近ますます注目度が上がっていますね。
なお、ロジカルシンキングの基礎から勉強したい場合は、以下のリンクを参考にしてください。
では始めましょう。
toc
「普遍的」とは
まずは「普遍的」という言葉の意味を明確にしましょう。辞書には以下のように書かれています。
広く行き渡るさま。極めて多くの物事にあてはまるさま。「生物に共通の—な性質」
この定義は正しいかもしれませんが、ロジカルシンキングを行ううえでは曖昧すぎて実用的ではありません。そこで、当サイトではもう少し限定的な定義を採用します。
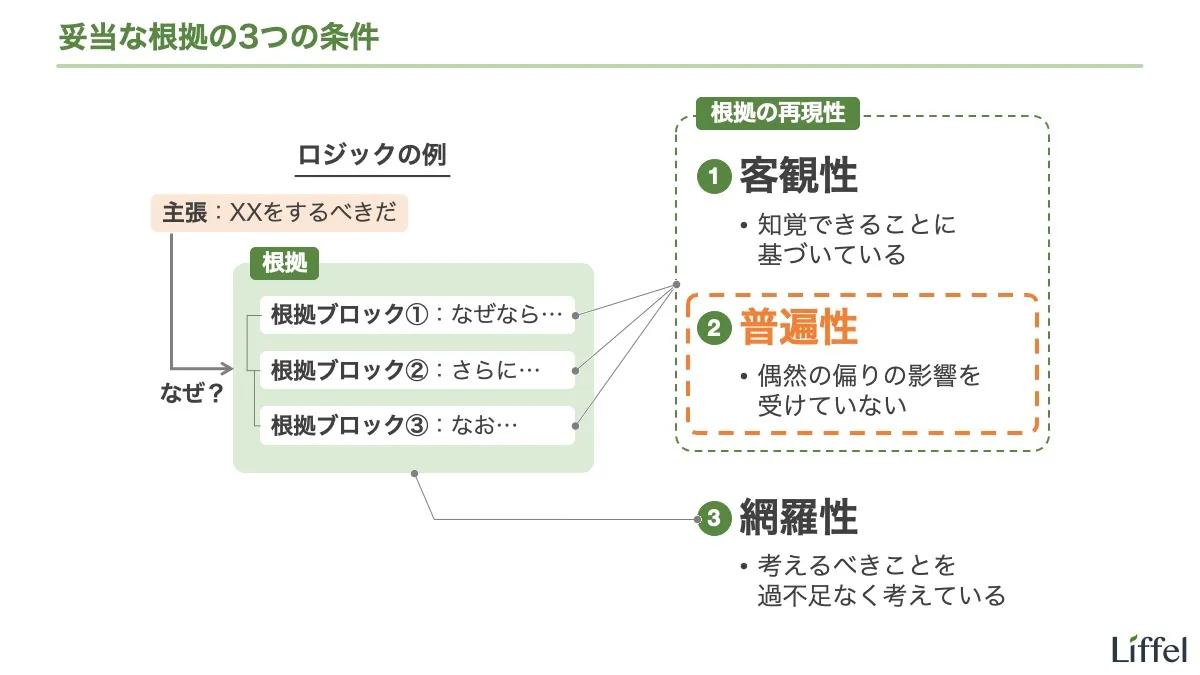
普遍的であるとは、偶然の偏りの影響を受けていないことです。ロジカルシンキングを行ううえでは、これを「普遍的」という言葉の意味だと考えてください。
普遍的：偶然の偏りの影響を受けていないこと
「偶然の偏りを受けていない」とは①
では、「偶然の偏りの影響を受けていない」とは、具体的にどういうことなのでしょう？
例を使って説明します。まずはこの主張を見てください。
主張：このサイコロは、必ず1が出るようにイカサマされている。
この主張に対する根拠の候補を、いくつか並べてみます。
- なぜなら、私がこのサイコロを振ったところ、1が出たからだ。
- なぜなら、私がこのサイコロを振ったところ、2回連続で1が出たからだ。
- なぜなら、私がこのサイコロを振ったところ、3回連続で1が出たからだ。
- なぜなら、私がこのサイコロを振ったところ、4回連続で1が出たからだ。
- なぜなら、私がこのサイコロを振ったところ、10回連続で1が出たからだ。
ここで質問です。あなたは、何番の根拠なら妥当だと思いますか？ 言い換えると、サイコロがイカサマされていると認めるためには、何回連続で1が出る必要があるでしょう？
まず、①ではお話になりませんよね。普通のサイコロでも、6回に1回は1が出るわけです。こんな根拠でサイコロがイカサマされていると主張するのは無理です。
②や③でも、主張を通すのは厳しいでしょう。普通のサイコロでも、2回連続で1が出る確率は1/36（約3%）、3回連続なら1/216（約0.5%）です。これくらいは、十分に起こり得る確率です。
しかし、⑤までいくと、今度はイカサマを疑わないほうが難しくなります。普通のサイコロを振って、10回連続で1がでる確率は6分の1の10乗、これは約0.00000165%です。ほとんどゼロですね。これなら、「このサイコロは必ず1が出るようにイカサマされている」と主張しても問題なさそうです。
「偶然の偏りを受けていない」とは②
ここまでの話を引いた目線で説明します。
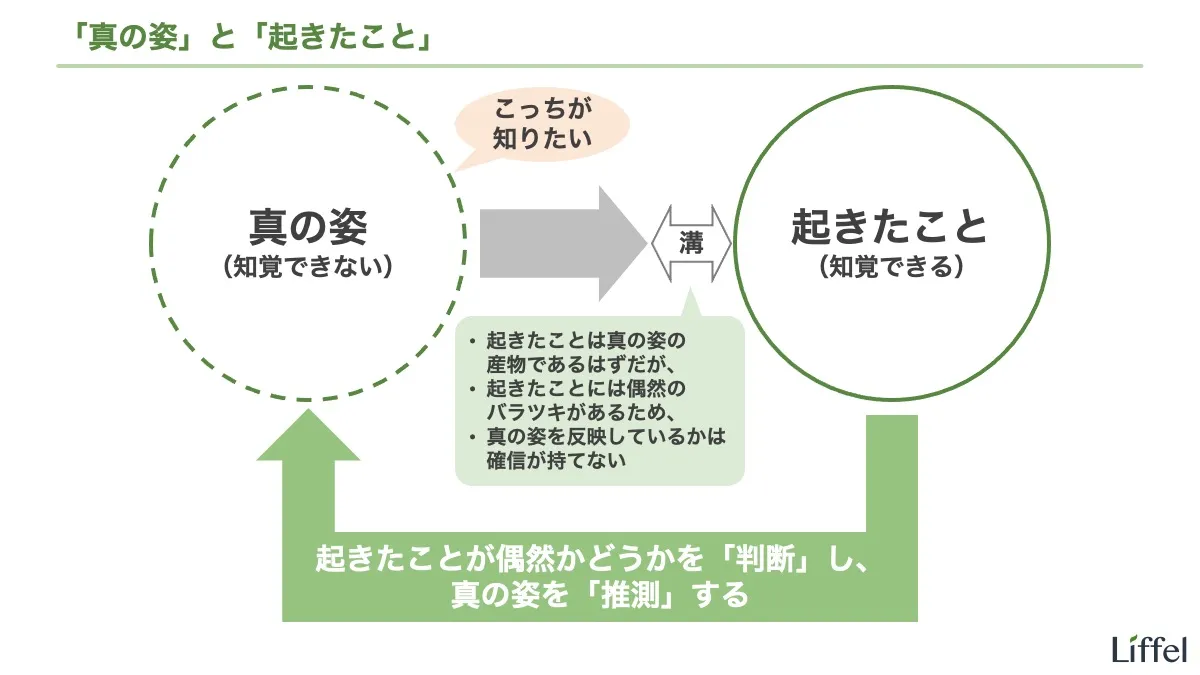
まず、「サイコロの本当の状態（イカサマされている/いない）」を、サイコロの「真の姿」と呼ぶことにします。
サイコロをどれだけ振っても、サイコロの真の姿を100パーセントの確度で断言することはできません。普通のサイコロでも、連続で1が出続ける確率はゼロにならないからです。100回でも、1億回でも、普通のサイコロで1が出続ける可能性はあります。
ちなみに、ここで「サイコロを分解すればいいでしょ」と思ったかもしれません。たしかに、サイコロであれば「サイコロを分解する」という方法によって真の姿を知ることができます。しかし、この後の例でも紹介しますが、世の中のほとんどのケースでは、真の姿を直接知る方法はありません。一旦、サイコロに関しても「分解はできない」ということにさせてください。
となると、観察できたこと（＝客観的な事実）から真の姿を推定するしかないわけです。今回の例なら、サイコロを振った結果から、サイコロの真の姿を推定します。
しかし、ここで1つの問題が生じます。観察できたことには偶然のバラツキがあるのです。観察できたことが「真の姿を反映している」のか、「たまたまそうなった」のかは、決して100パーセントの確度では分かりません。
サイコロの例で説明しましょう。先ほど説明したとおり、普通のサイコロであっても連続で1が出続けることはありえます。つまり、「1がX回連続で出た」という「起きたこと」と、「サイコロがイカサマされている/いない」という「真の姿」の間には、どこまで行っても埋められない溝があるのです。
では、どうしたらよいのでしょう？ 答えを言うと、この溝を埋めるのは、私たちの判断です。「いや、これは単なる偶然だろう」、「さすがにこれは偶然とは考えられない」という判断を、私たちがするしかありません。
先ほどの例では、「サイコロがイカサマされていると認めるためには、何回連続で1が出る必要があるでしょう？」と聞きました。これは言い換えれば、「何回連続で1が出た時点で、あなたはそれを『偶然ではない』と判断しますか？」ということです。問われているのは、「偶然かどうか」に対するあなたの判断です。
このように、「観察できたこと」と「真の姿」の間にある埋められない溝を、判断というジャンプで飛び越えるのです。
観察できたことが偶然かどうかを「判断」して、真の姿を推測する
一般的なケース
ここまでの話を、サイコロよりも一般的なケースで確認しましょう。
X社とY社、どちらのデザインが優れているだろうか？
X社だよ。私の周りの5人にアンケートした結果、3人がX社のデザインが好きだと答えたよ。
それって、1人が意見を変えるだけで結果が逆になるじゃないか。あてにならないよ。
ここで確認してほしいのは、以下の3点です。
- 「どちらのデザインが優れているか」を、直接観察することはできない（真の姿を直接知ることはできない）
- そこでパンダは、「どちらのデザインが好きか」をアンケートし、そのデータを根拠として、真の姿を推測（主張）している
- しかし、クマはパンダの用意したデータが「偶然の偏りの影響を受けている」と判断し、パンダの主張を棄却した
つまり、クマは「パンダの用意した根拠は客観的ではあっても、普遍性を欠いている（偶然の偏りの影響を受けている）」と判断したわけです。その結果として、パンダの主張（X社のデザインの方が優れている）は棄却されてしまいました。
では、どうしたらクマを説得できるのでしょう？ 答えは明らかで、「偶然の偏りの影響を受けていない」と判断される根拠を用意すればいいのです。
この場合は、回答者の数を増やせばいいです。詳しい説明はカットしますが、回答者の数を増やすことで、偶然の偏りの影響を受けているとは考えられなくなります（＝普遍性が高まる）。厳密にはこれだけでは不十分なのですが（サンプルの構成なども考慮する必要がある）、とりあえず難しい話は抜きにして、回答者の数を増やしてみましょう。
X社とY社、どちらのデザインが優れているだろうか？
X社だよ。私の周りの1000人にアンケートした結果、600人がX社のデザインが好きだと答えたよ。
それなら、たしかに「X社のデザインが優れている」と言えそうだね。
今度は主張を通すことに成功しました。
では、先ほどと何が変わったのでしょう？
もちろん、表面的に変わったのは「回答者の数」です。こんどは、1人が意見を変えたところで結果はビクともしないですからね。
しかし、本質的に変わったのは普遍性に対する判断です。回答者の数が変わった結果、クマの「パンダの提示した根拠の普遍性に対する判断」が変わったのです。ここを押さえてください。
統計学
では、どうやって根拠の普遍性（＝提示された根拠が偶然の偏りの影響を受けているか）を判断すればよいのでしょう？
この判断の方法を学ぶのが、統計学という学問です。統計学というと、何やら難しい数式をこねくり回すイメージを持っている人も多いと思いますが、もっともシンプルに統計学を表現するなら、「起きたことが偶然かどうかを判断する方法」になると私は思います1。
統計学：起きたことが偶然かどうかを判断する方法
ここまでの話をまとめると、普遍的な根拠とは、「偶然の偏りの影響を受けていない」と判断される、客観的な根拠の集合のことです。そして、偶然の偏りの影響を受けているかの判断を行うには、統計学の知識が必要となります。
なぜ普遍的な根拠が妥当なのか
なぜ、普遍的な根拠は妥当なのでしょう？ 言い換えると、なぜ、偶然の偏りの影響を受けていない根拠は批判に耐えぬけるのでしょうか？
答えを先に言うと、そういうルールにしているからです。「統計学的な計算の結果『偶然の偏りの影響を受けていない』と判断される根拠」は妥当であると認めるのが、世の中の一般的なルールです。
といっても、これは頭のいい人たちが勝手に決めたムチャクチャなルールだというわけではありません。私の知るかぎり、これはもっともフェアな考え方です。
なぜ統計学に頼って判断することがフェアなのか
先述のとおり、「起きたこと」から「真の姿」を推測するには、どうしても私たちの「偶然かどうかの判断」が必要になります。
ここで、さまざまな論点に対し、この判断を私たちが好き勝手にすると、集団で考えることは不可能になります。自分の都合に応じて判断基準を変えればいいですからね。
「確率はゼロではない」
これのもっとも分かりやすい例が、「確率はゼロではない」という難癖です。これは、自分に都合の悪い主張を支える普遍的な根拠が出てきたときに使われる、典型的で、意味のない反論です。
先ほどのサイコロのケースで考えてみましょう。たとえば、どうしてもサイコロがイカサマされていると認めたくないなら、100回連続で1が出たあとに「普通のサイコロで、100回連続で1が出る確率はゼロではない」と言い張ることは可能です。
実際、確率はゼロではありません。「100万の10乗」分の1くらいの確率で、普通のサイコロでも100回連続で1が出ます。
しかし、いかに「確率はゼロではない」が数学的に正しいとしても、こんな判断をする人と一緒に考えたくはないですよね。こんな確率は、人類が猿から人になるまでサイコロを振り続けても、一度も起こらないレベルに「ほぼゼロ」です（テキトーですが）。こんな言い分を認めていては、真の姿を明らかにすることは決してできません。
サイコロ以外の例も見ておきましょう。
宝くじの一等に当たる確率はゼロではない。今すぐ、全財産を宝くじにつぎ込むべきだ。
この病気で死んだ人は今まで一人もいないが、あなたが最初の一人になる確率はゼロではない。予防のためにこの薬を飲みなさい。
外を歩いていて、隕石が直撃して死ぬ確率はゼロではない。家から一歩も出るべきではない。
どれも、「確率はゼロではない」の部分は正しいことを確認してください。それでも、その後に続く主張は、どれも正しくはありませんよね。
こうなる理由は、「確率はゼロではない」ことはほぼすべての確率事象に言えてしまうからです。言い換えると、この言説はあらゆることに当てはまるため、正しくても無意味なのです。当然、この言説は根拠として主張の正しさを支えることに、何の貢献もしていません。
この論法への対応策は大きく分けると以下の2つです。
- 具体的な確率を計算する
- 反対事象・他事象に対しても「確率はゼロではない」ことを指摘する
参考までに、上記の例に対する反論例を挙げておきます。
宝くじの一等に当たる確率はゼロではない。今すぐ、全財産を宝くじにつぎ込むべきだ。
宝くじの一等が当たる確率は公表されているよ。一等の期待値を計算してみるといい。
この病気で死んだ人は今まで一人もいないが、あなたが最初の一人になる確率はゼロではない。予防のためにこの薬を飲みなさい。
その薬を飲んで死ぬ確率もゼロではないと思いますが、なぜ、薬を飲んだほうが良いと言い切れるのです？
外を歩いていて、隕石が直撃して死ぬ確率はゼロではない。家から一歩も出るべきではない。
外を歩いていて、とても素敵なことが起こる確率もゼロではない。私はそっちを選ぶよ。
ただ、私の経験上、人が「確率はゼロではない」と言い出すときには、すでに感情的になっており、まともな議論になりません。典型的なのはギャンブルですね。私もよく、以下のように考えていました。
この次の勝負で一発逆転が起きる可能性はゼロではない。倍プッシュだ！
今でも、このように考えてしまう確率はゼロではありません笑
どうすればいいか
では、どうしたらこのような「確率に対する恣意的な判断」を防ぎ、建設的に考えることができるのでしょう？
答えは、判断の基準を事前に揃えることです。「ここまでは偶然、ここから先は偶然とは考えない」という合意が事前になされていれば、結果によって偶然かどうかの判断を都合よく変える事態を防げます。これならフェアですよね。
統計学を学ぶ意義
ここまで述べたことが、統計学を学ぶ意義です。統計学で学ぶことは、まさに先ほど述べた「判断の基準」です。つまり、統計学を学ぶことで、「偶然かどうかの判断」に参加できるようになります。
というわけで、普遍的な根拠を批判・構築するためには、統計学を学ぶしかありません。
普遍的な根拠を批判・構築できるようになりたいなら、統計学を学ぶしかない
そして、統計学は一朝一夕には理解できません。理論を学び、実際にデータを自分で触って検定などを実施しないことには、「どういう事実の集合を集めれば、『たまたまそうなっただけじゃないの？』という批判を退けられる根拠になるのか」は分からないのです。
つまり、一朝一夕には、普遍的な根拠を批判・構築する方法は学べません。当サイトでは統計学に深入りする予定は今のところないので、自分で別途勉強してください。
ただ、これで終わっては寂しいので、統計学の基礎について簡単に勉強しましょう（後日投稿予定）。
さらに学習を進めたい人は
ここまで読んでいただき、どうもありがとうございました。ロジカルシンキング学習をさらに進めたい人は、以下のエントリーに進んでください。網羅的な根拠について説明しています。
また、ロジカルシンキング関連のエントリーは以下のページにまとめてあります。こちらも参考にしてください。
Footnotes
-
統計学という学問は、平均や分散といった「データの特徴を明らかにする方法」を学ぶ「記述統計学」と、本文中で述べたように「データが偶然かを判断する方法」を学ぶ「推測統計学」に分かれています。厳密には、ここで述べているのは推測統計学のことです。 ↩