このエントリーでは、自力で論点を分解する方法の全体像を学びましょう。
フレームワークは便利なものですが、実践のロジカルシンキングにおいてフレームワークだけで論点を分解しきれるとは限りません。詳しくは後述しますが、個別具体的で難しい論点ほど、フレームワークに頼れなくなります。
そのような場合に頼れるのは、あなた自身の論点を分解する力だけです。自力で論点を分解するとはどういうことなのか、そこで使えるテクニックにはどのようなものがあるかを学びましょう。
なお、フレームワークについては理解できている前提で話を進めます。もし「フレームワーク」がよく分からない場合は、事前に以下のリンクを読んでください。
では始めましょう。
toc
「自力で論点を分解する」とは

まずは、論点を分解する2つの方法を復習しましょう。
スライドにあるように、論点を分解する方法は以下の2つです。
- フレームワークを利用する
- 自力で分解する
今回はこのうち、「②自力で分解する」を掘り下げます。これは言葉どおり、フレームワークに頼らず、自分の力で論点を分解することです。
フレームワーク vs 自力での分解
フレームワークと比較して、自力で論点を分解することにはどのような特徴があるのでしょう?
結論を先に言うと、自力で論点を分解することにメリットはありません。単に、ほとんどの論点はフレームワークだけでは掘り下げきれないので、自力で分解するしかないだけです。
もう一度、先ほどのスライドを見てください。

見てのとおり、自力で分解することには多くのリスクがつきまといます。分解が網羅的になるかも、問題解決につながるかも分かりません。分解が失敗だとその後の作業は無意味なものになるので、これはとてつもないリスクだと言えます。
よって、論点を分解するときには、まずはフレームワークが適用できないか考えましょう。フレームワークが適用可能な論点に対して、自力で分解する理由は存在しません。よく「フレームワークに頼らずに、自分の頭で考えよう」といった言説を見かけますが、これには何の根拠もないので気にしないでください。どのように論点を分解しようが、問題が解決すればよいのです。
もちろん、すでに解説したように世の中には偽フレームワークがたくさんある上に、正しいフレームワークを正しく使うこともそんなに簡単ではありません。それでも、自力で分解するよりずっと楽なのは確実です。まずはフレームワークに習熟することを優先してください。
まずはフレームワークが使えないか考える
フレームワークに頼れない論点
では、自力で分解することの出番はないかというと、そんなことはありません。私たちが扱う論点の大半は、フレームワークだけでは分解しきれないからです。以下、フレームワークに頼れない状況を確認していきましょう。
フレームワークに頼れない状況①:まだ誰も解いていないタイプの論点
まず、まだ誰も解いていないタイプの論点には、当然ながら使えるフレームワークが存在しません。
あるフレームワークが存在するということは、そのフレームワークの発明者が同じタイプの論点を解いたことを意味します。それでうまくいったから、フレームワークとして残っているわけですからね。
ということは、まだ誰も解いていないタイプの論点には、使えるフレームワークがありません。最高難易度の論点を考えるときには、フレームワークには頼れないわけです。
フレームワークに頼れない状況②:とても小さい(個別具体的な)論点
フレームワークとは汎用的な公式のことなので、個別具体的な状況に対応できるフレームワークというのは、定義により存在しません。言い換えると、フレームワークで分解できるのは論点のハイレベル(粗く、抽象的)なところまでで、ローレベル(細かく、具体的)な部分は分解できないのです。以下のスライドでイメージを掴んでください。
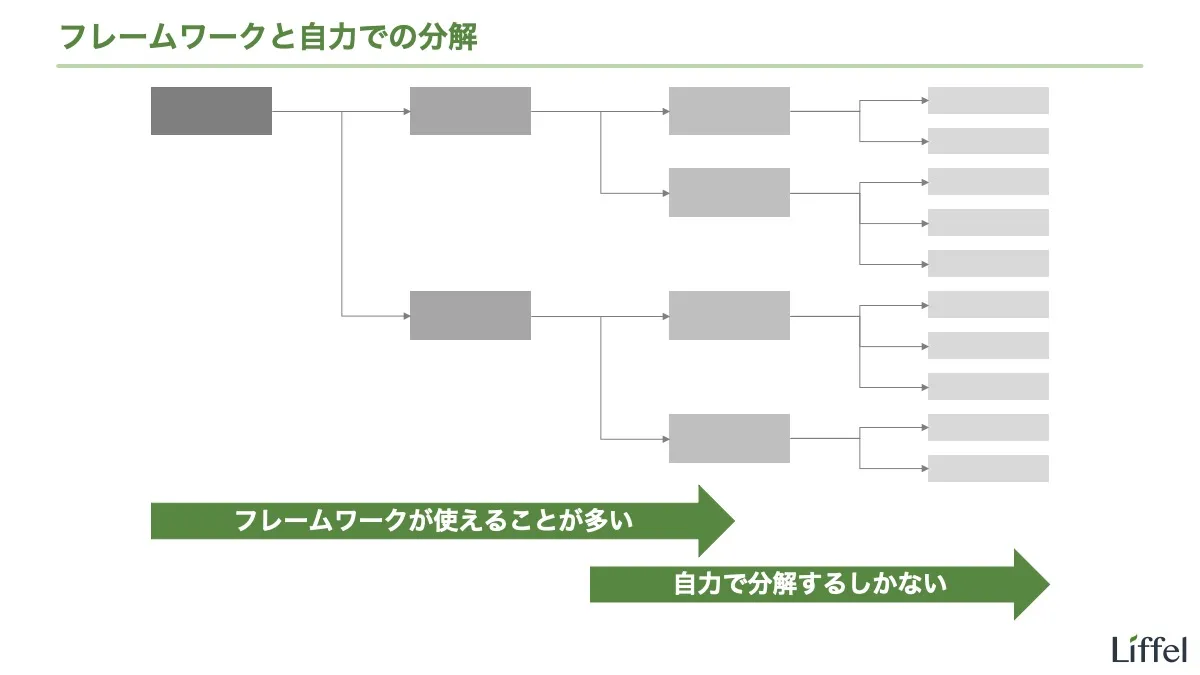
そして、論点に対して正しい答えが出せるかは、ローレベルの分解がうまくいくかにかかっています。ハイレベルな分解だけでは雑になってしまいますからね。丁寧に考えるためには、フレームワークの先に降りていくしかありません。さまざまな切り口を試し、問題解決につながる分解を見つけ出せるかが、あなたの腕の見せどころです。
自力で論点を分解する方法の全体像
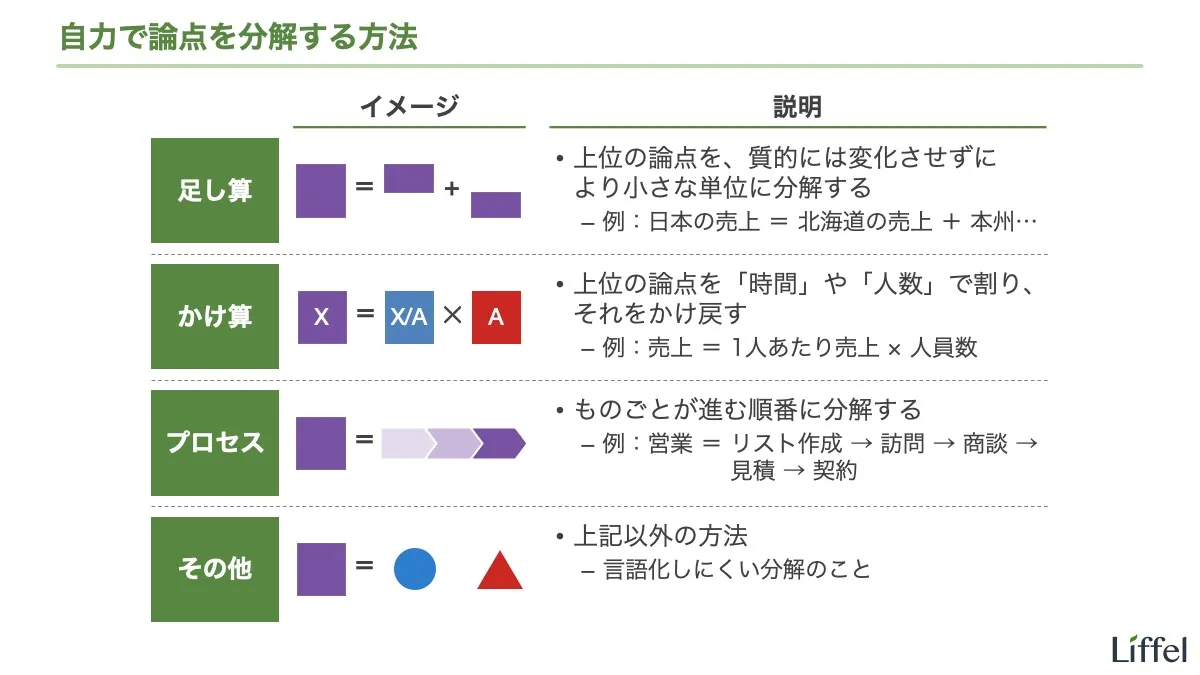
ここからは、自力で論点を分解する具体的な方法を見ていきましょう。全体像を以下のスライドにまとめました。

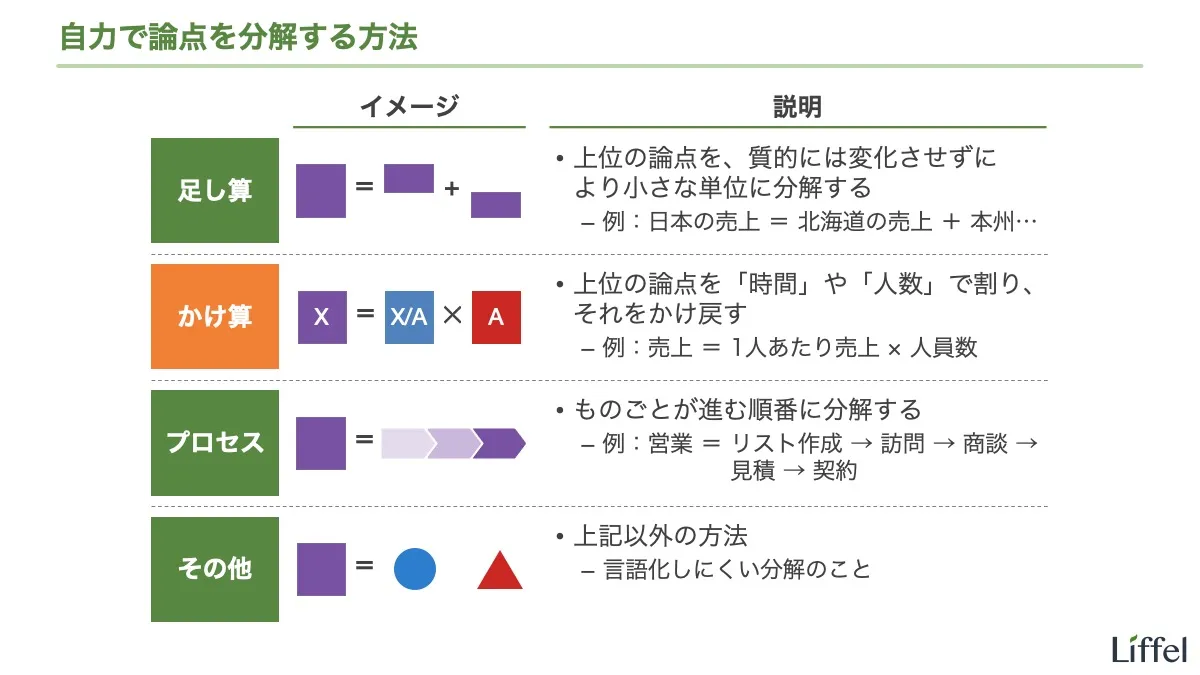
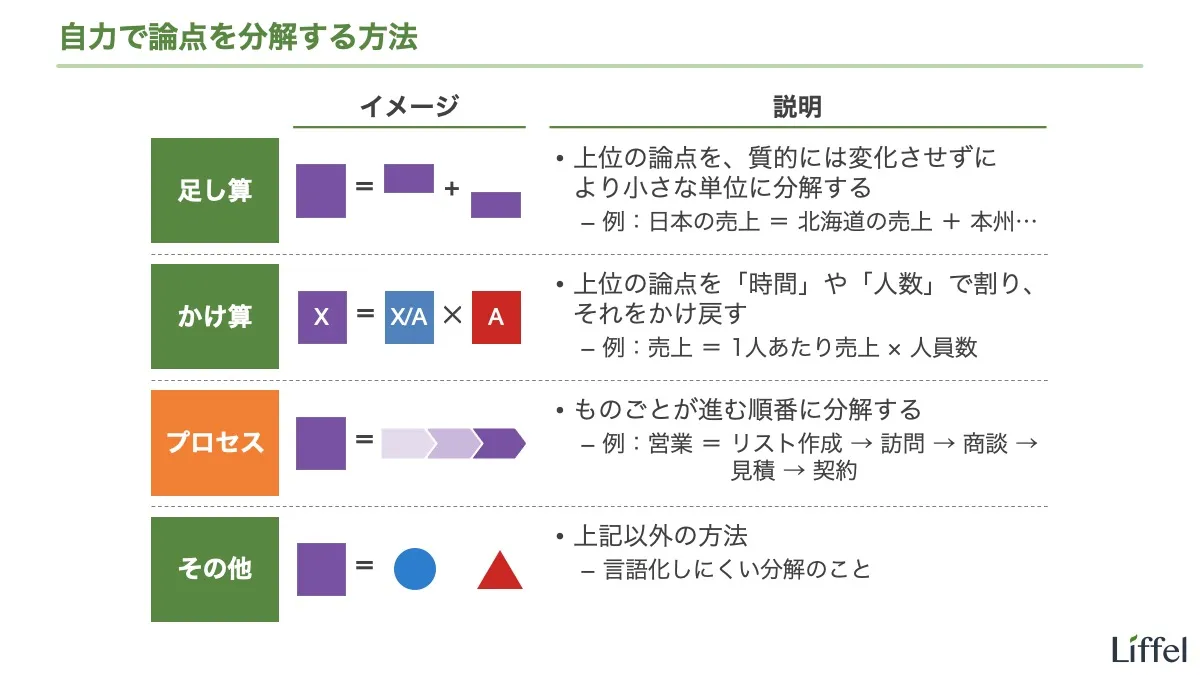
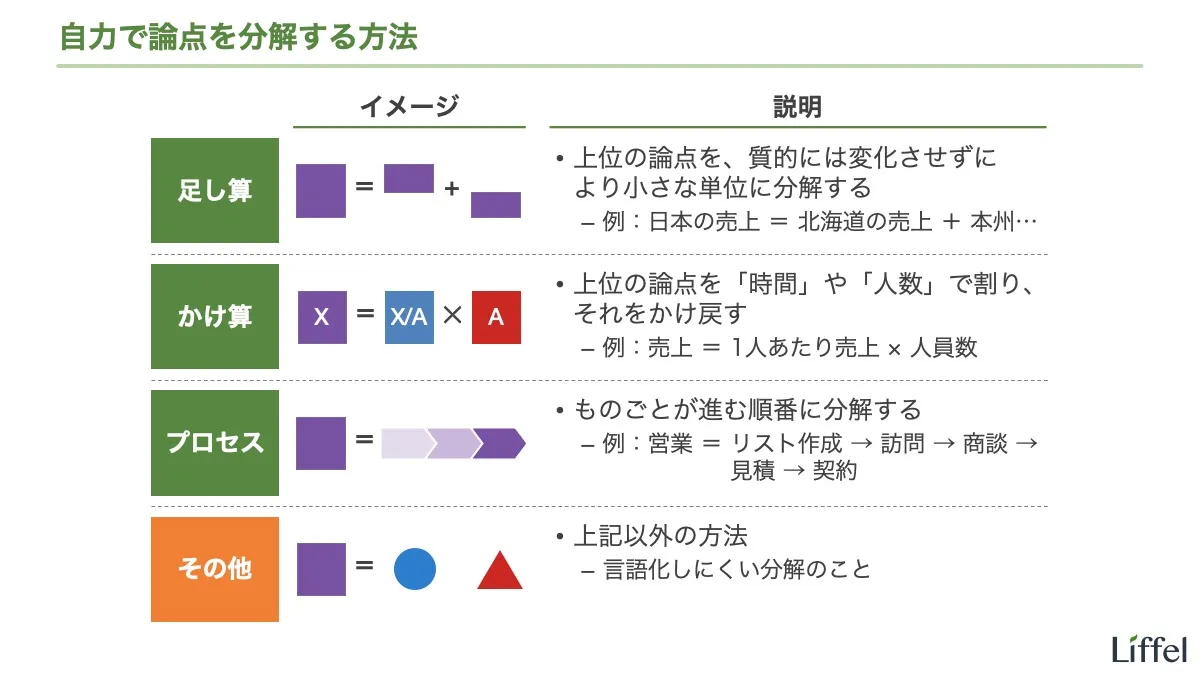
このように、自力で論点を分解する方法は大きく分けて4つあります。
- 足し算
- かけ算
- プロセス
- その他
①足し算、②かけ算、③プロセスの3つは、フレームワークほど固定的ではなくとも、自力で論点を分解する際に役立つテクニック(発想のヒント)です。便利なのでこの機会に覚えてください。個々の詳細は別エントリーで解説します。
④その他は、要するにガチンコです。正真正銘、何にも頼らずに自分の力で分解するということですね。
順に見ていきましょう。
自力で論点を分解する方法①:足し算
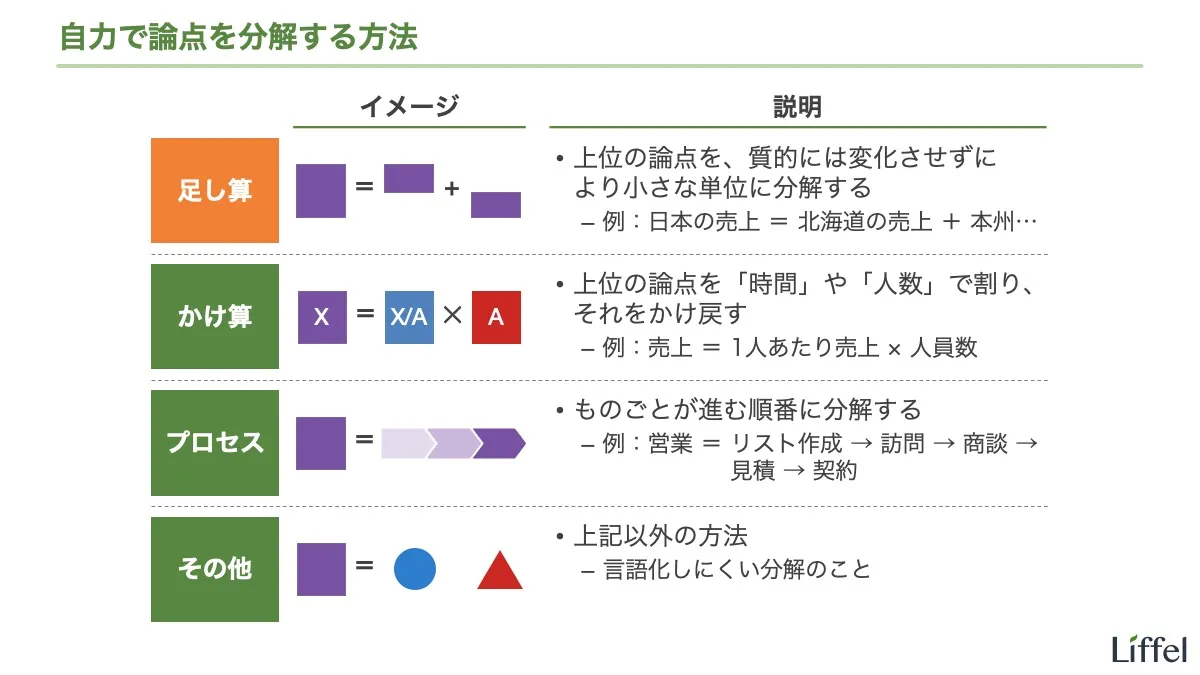
自力で論点を分解する1つめの方法は、足し算です。
足し算の分解とは、上位の論点を、質的には変化させずに、より小さな単位に分ける分解です。
具体例を見てみましょう。
- 日本の売上はいくらか?
- 北海道の売上はいくらか?
- 本州の売上はいくらか?
- 九州の売上はいくらか?
- 四国の売上はいくらか?
- 沖縄の売上はいくらか?
この例では、「日本」という上位の論点を「地域」という切り口でさらに小さな単位に分解しています。
上位の論点も下位の論点も「売上」を扱っており、質的には変化していないことを確認してください。下位の論点は、その売上を集計する範囲が小さくなっているだけです。このような分解が、足し算の分解です。
上位の論点を、質的には変化させずに、より小さな単位に分ける分解
自力で論点を分解する方法②:かけ算
自力で論点を分解する2つめの方法は、かけ算です。
かけ算の分解とは、上位の論点をある要素で割り、その要素をかけ戻す分解です。数式的に書くと、X = X/A ✕ Aと分解するわけですね。割る要素(数式のA)として使うのは「人数」か「時間」が多いです。
具体例を見てみましょう。
- 日本の売上はいくらか?
- 従業員1人あたりの売上はいくらか?
- 従業員は何人か?
この分解では、「売上」を「従業員数」という要素で割り、その後で「従業員数」をかけ戻しています。数式で表現すると「売上 =(売上/従業員数)✕ 従業員数」ということです。このような分解が、かけ算の分解です。
上位の論点をある要素で割り、その要素をかけ戻す分解
自力で論点を分解する方法③:プロセス
自力で論点を分解する3つめの方法は、プロセスです。
プロセスの分解とは、その名のとおりモノゴトが進む順番による分解です。
具体例を見てみましょう。
- どうしたら売上を増やせるか?
- どうしたら、リスト(見込み客の数)を増やせるか?
- どうしたら、リスト客の訪問数を増やせるか?
- どうしたら、商談率(訪問→商談の割合)を高められるか?
- どうしたら、見積率(商談→見積の割合)を高められるか?
- どうしたら、契約率(見積→契約の割合)を高められるか?
これはスライド内の例を論点の形で記述したものです。営業が「リスト作成→訪問→商談→見積→契約」と進む商品であれば、それぞれのプロセスの試行回数や成功率を高められれば、最終的な売上も増えますよね。このような分解がプロセスによる分解です。
モノゴトが進む順番による分解
自力で論点を分解する方法④:その他
最後の方法は「その他」です。「その他」がどういう分解かを説明することはできません。説明できない自力の分解のことを「その他」と呼んでいるからです。
大半のフレームワークは、「その他」による分解です。例として、「成果 = 努力 ✕ 才能 ✕ 運」のフレームワークを見てみましょう。
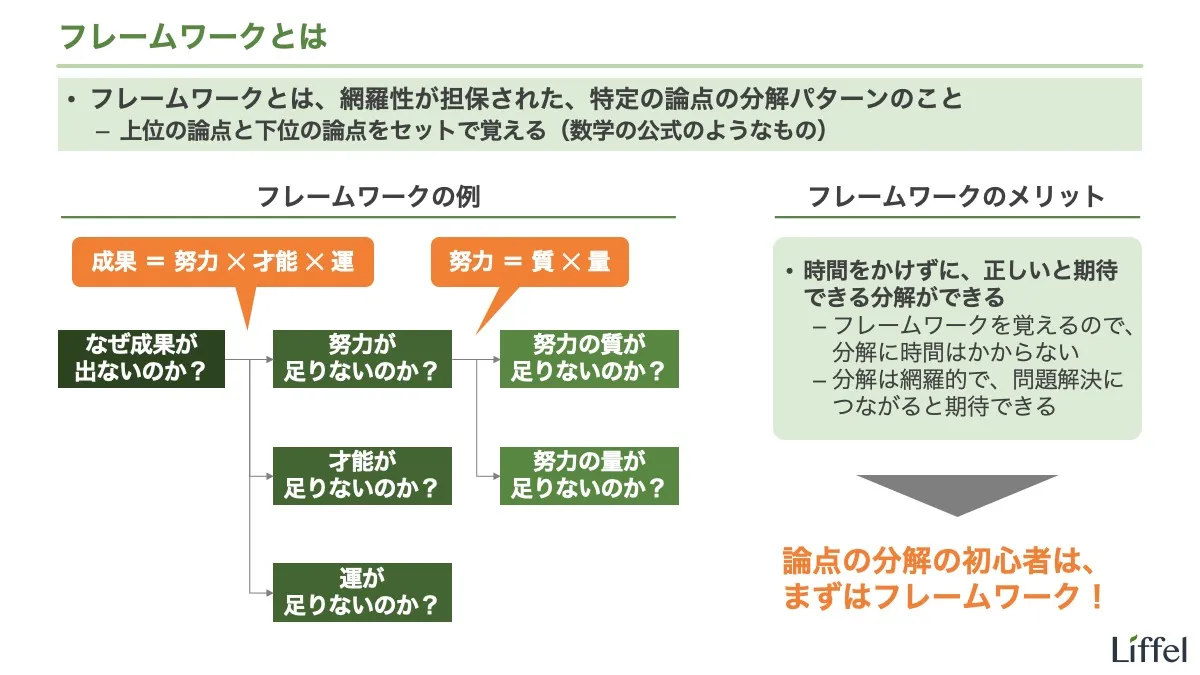
まず、この分解は足し算ではありません。分解の前後で質的に変化しているからです。また、明らかにかけ算やプロセスでもないですよね(かけ算マークを使用していますが、これは表現上の理由)。つまり、これまでに紹介したどの方法でもないということです。このような分解が「その他」の分解です。
この分解がもっともハードであることは言うまでもありませんが、その分、これで綺麗に分解できたときはスパッと問題を解決できることが多いです1。下手をすると、あなたの名前を冠したフレームワークが生まれる可能性すらあるので、食わず嫌いをせずに、チャレンジしてみてくださいね。
以上、自力で論点を分解する方法の全体像を説明しました。次回から個別の分解方法を掘り下げていきましょう。まずは足し算からです。
また、ロジカルシンキング関連のエントリーは以下のページにまとめてあります。こちらも参考にしてください。
Footnotes
-
厳密には、スパッと問題解決ができることは「その他」で分解するうえでの必要条件です。フレームワークにも、足し算やかけ算といった発想のヒントにも頼らず分解する以上、スパッと問題を解決できないなら、そのような「その他」の分解には正当性がまったくありません。そういう意味でも、「その他」の分解はもっともシビアです。 ↩