このエントリーでは、問題を評価するとはどういうことかを学びましょう。
問題を評価し、考えるべき論点を正しく選べることは、極めて重要なことです。間違った論点を考えても、何も生まれませんからね。完全なリソースの無駄です。
よって、「間違った」論点とはどのような論点なのか、「正しく」問題を評価するとはどういうことなのかを考えておく必要があるのです。率直に言って、簡単な内容ではありませんし、正解があるような話でもないのですが、頑張っていきましょう。
なお、このエントリーは論点設定の全体プロセスを理解していることを前提としています。先に以下のエントリーを読んでおいてください。
では始めましょう。
toc
問題を評価するとは
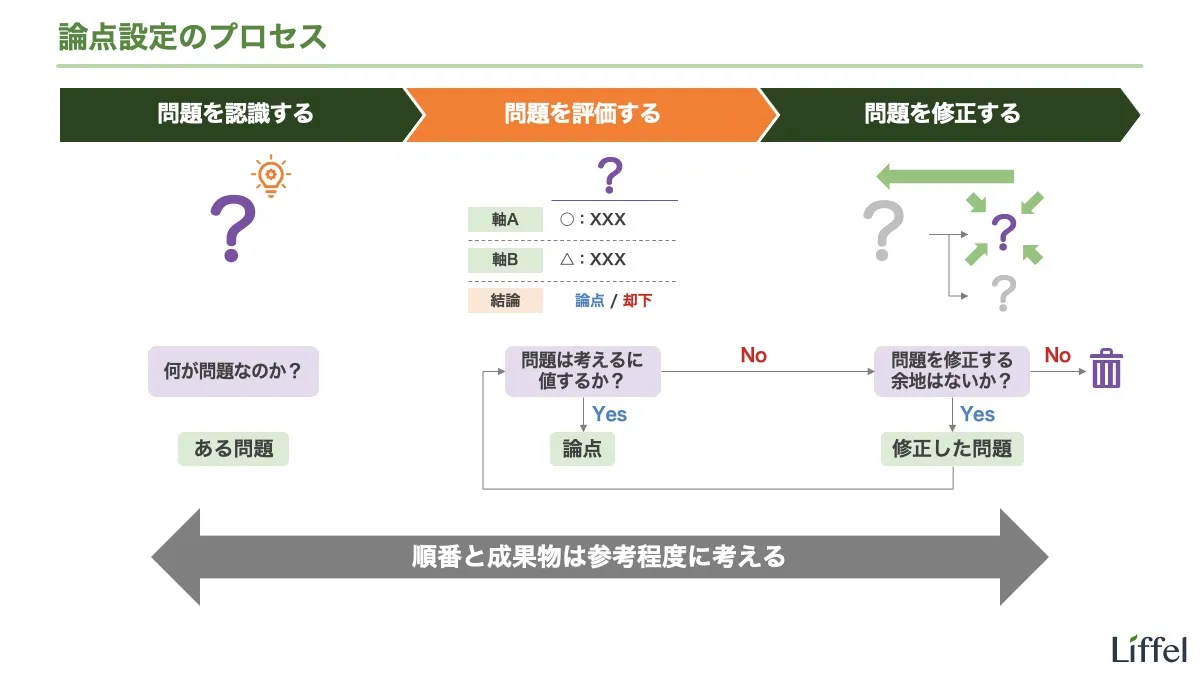
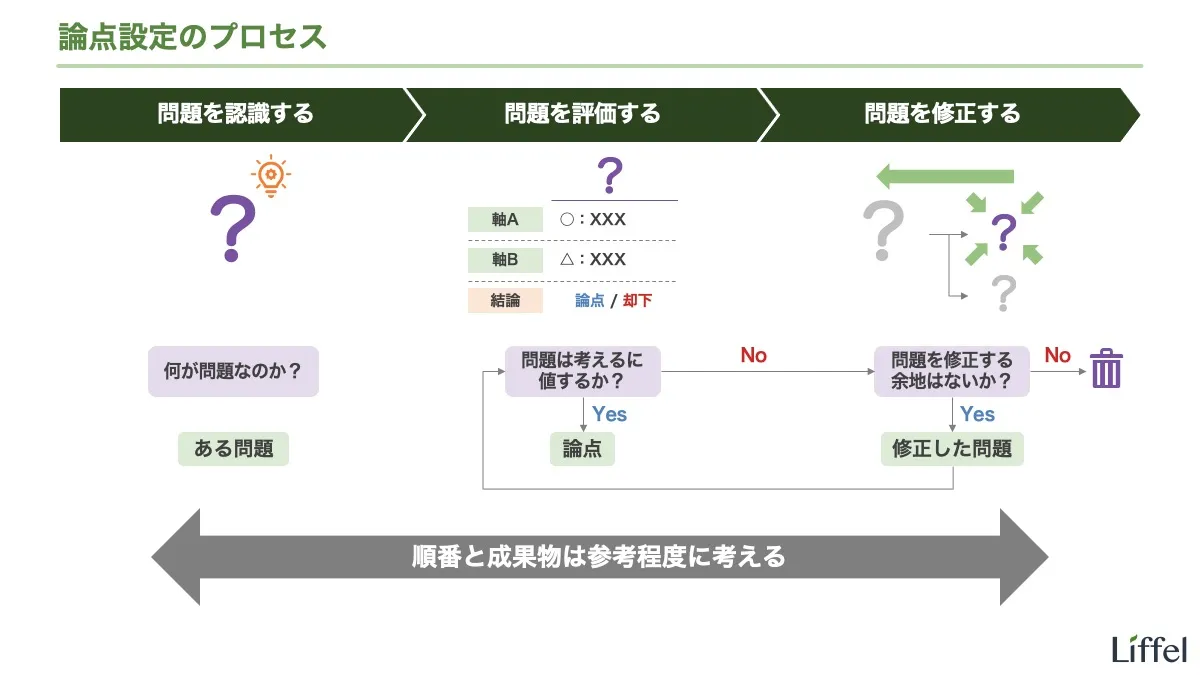
問題を評価することは、論点設定における2つめのプロセスです。認識した問題をそのまま論点にするのではなく、その問題は考えるに値するかを、意識的に検討します。
具体的に何をするか｜インパクト期待値とは
では、問題を評価するとは、具体的に何をすることなのでしょう？
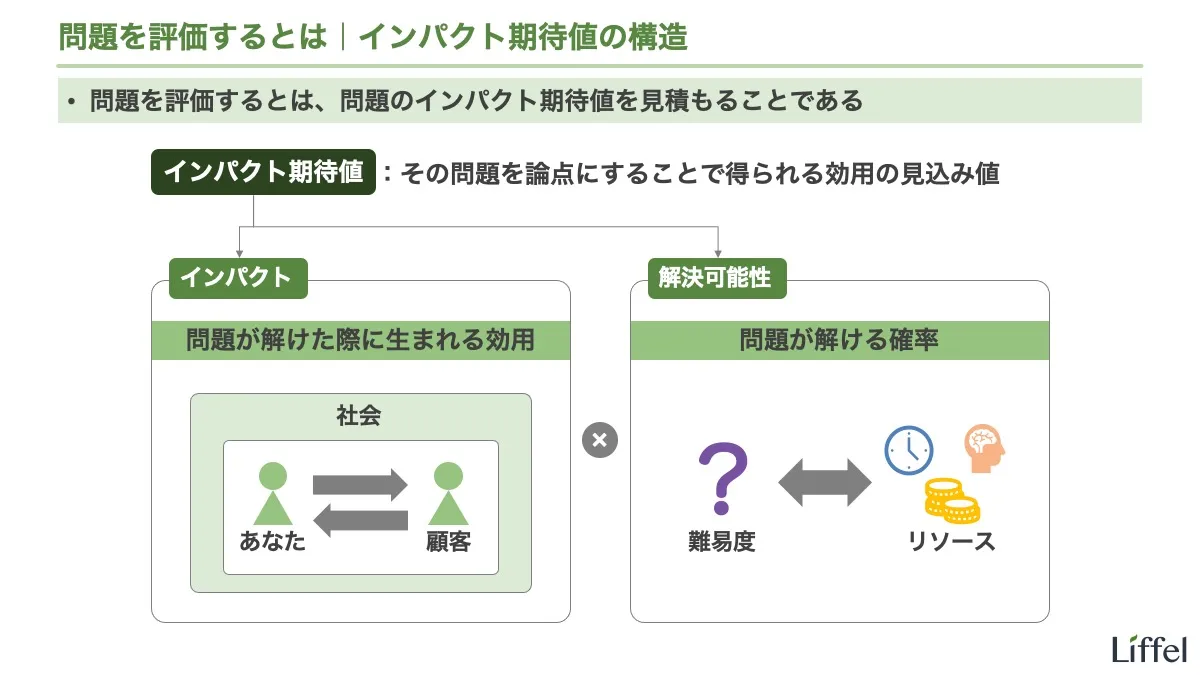
答えを先に述べると、問題を評価するとは、問題のインパクト期待値を見積もることです。以下のスライドを見てください。
内容がてんこ盛りのスライドなので、ここではサッと目を通すだけで十分です。これから数回のエントリーを使って、このスライドを掘り下げていきましょう。
まず定義ですが、インパクト期待値とは、「その問題を論点にすることで得られる効用の見込み値」のことです。問題から得られるインパクトに、解ける確率を掛けるわけですね。要するに数学の「期待値」のことなのですが、実際に値を計算できるわけではないので別の言葉にしてあります。
この値を見積もることが、「問題を評価する」プロセスにおけるゴールです。なお、「インパクト期待値」という言葉は私の造語ですので注意してください。
問題を評価するとは、問題のインパクト期待値（その問題を論点にすることで得られる効用の見込み値）を見積もることである
テストとインパクト期待値
先に具体例を見てみましょう。あなたはおそらく、すでにインパクト期待値を見積もった経験があります。一般に、テストにおいてインパクト期待値を見積もるからです。
テストにおいて、「前から順に取り組んで、解けるまで先に進まない」なんて戦略を採用する人はいませんよね。それでは、前半に解けない問題があった場合、そこでゲームセットになってしまいます。最低でも、「まずは出題順に解くが、それなりに時間を使って解けない問題は諦めて、先に進む。すべての問題に取り組んだ後で時間が余っていれば、解けなかった問題に再度取り組む」という戦略になるはずです。
これはまさに、インパクト期待値の見積もりそのものです。知ってのとおり、テストでは解けなかった問題は点数（インパクト）が貰えません。よって、解けるかどうか（解決可能性）を判断して、その結果に従って「どの問題を考えるか」を変えているわけです。
大学受験の数学などでは、もっと露骨にインパクト期待値の見積もりをすることもあります。「最初の30分ですべての問題を少しだけ考えて、難易度に順位をつける。それから、簡単そうな問題から順に解いていく」というものです。この戦略だと確実に得点できるため、大事故を回避できます1。
このように、インパクト期待値を見積もることは、あなたも既に経験している可能性が高いです。あまり難しく考えないでください。
ただし、学校のテストと、実社会で考える問題では、以下の2点が大きく異なります。
- テストではインパクト（点数）は与えられるもので数値化もされているが、実社会の問題ではインパクトを自分で決めなければならず、かつ数値化もできない
- テストで「誰が考えても答えが出せない問題」は絶対に出題されないが、実社会では解決可能性がゼロである問題はよくある
というわけで、実社会の問題でインパクト期待値を見積もることは、テストほど簡単ではありません。だからこそ、意識的に、慎重に問題を評価する意義があるのです。
インパクト期待値の構造
では、インパクト期待値の構造を細かく見ていきましょう。といっても、すべてを説明していると終わらなくなるので、このエントリーでは大きな構造の説明に留めます。先ほどのスライドを確認してください。
このように、インパクト期待値は、「インパクト」と「解決可能性」のかけ算で決まります。
インパクト期待値 ＝ インパクト × 解決可能性
これは数学における「期待値」の概念をそのまま適用しただけなので問題ないでしょう。忘れてしまった人は下記を参考にしてください。
期待値とは、1回の試行で得られる値の平均値のことで、得られうるすべての値とそれが起こる確率の積を足し合わせたものです。
この説明における「得られうるすべての値」がインパクト期待値における「インパクト」であり、「それが起こる確率」が「解決可能性」です。
なお、実際のインパクト期待値は数字では表現できません。分かりやすさのために数学的な表現を使用しているだけです。これ以降も「値」、「計算する」といった表現が多用されますが、あくまで比喩的なものです。
まだピンとこないかもしれませんが、とりあえず先に進みましょう。細かく見ていくうちに分かるはずです。
インパクトとは
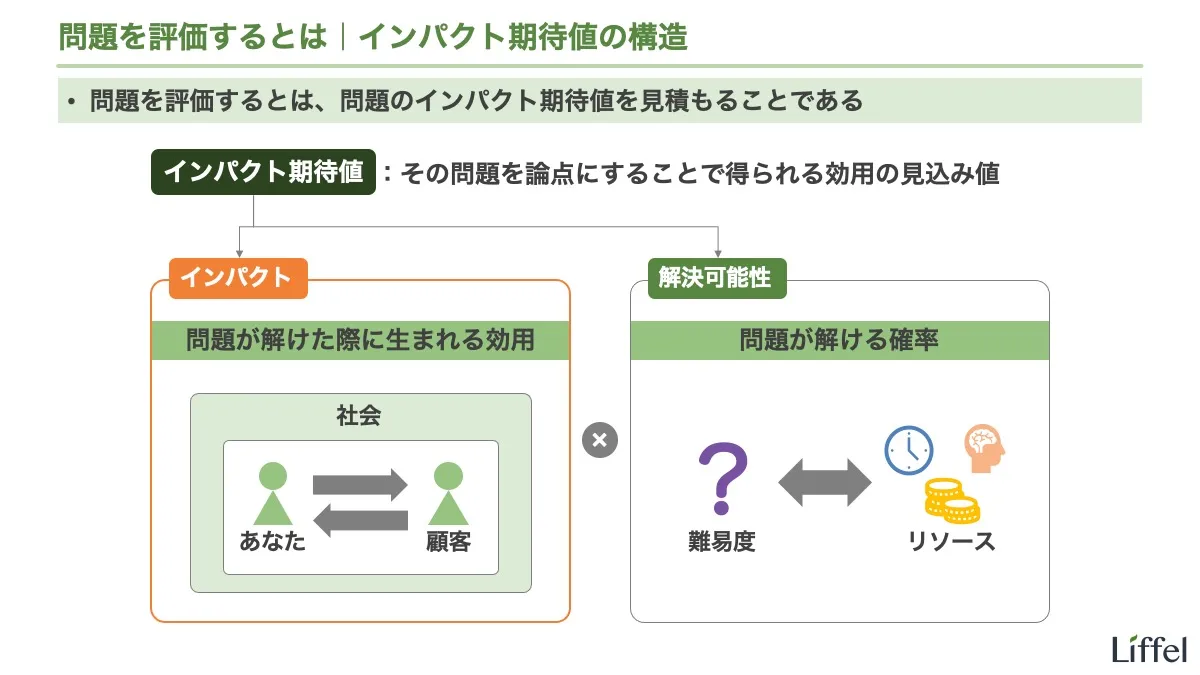
では、要素を順に見ていきましょう。まずはインパクトからです。
インパクトとは、その問題が解けた際に得られる効用のことです。先述のとおり、いわゆる「価値」のことだと考えてください。具体的には、以下の要素をすべて足し合わせた概念です。
- あなた（自分自身）へのインパクト
- 知的好奇心の充足
- 金銭的報酬
- その他の欲求の充足
- 顧客へのインパクト
- 社会へのインパクト
最もイメージしやすいのは、知的好奇心の充足でしょう。たとえば、難しい数学の問題が解けたら嬉しいですよね。このような、「問題が解けた際に生じる嬉しい/ありがたいこと」を総体として捉えたものが、ここでの「インパクト」です。
インパクト：その問題が解けた際に得られる効用（の総体）
解決可能性とは
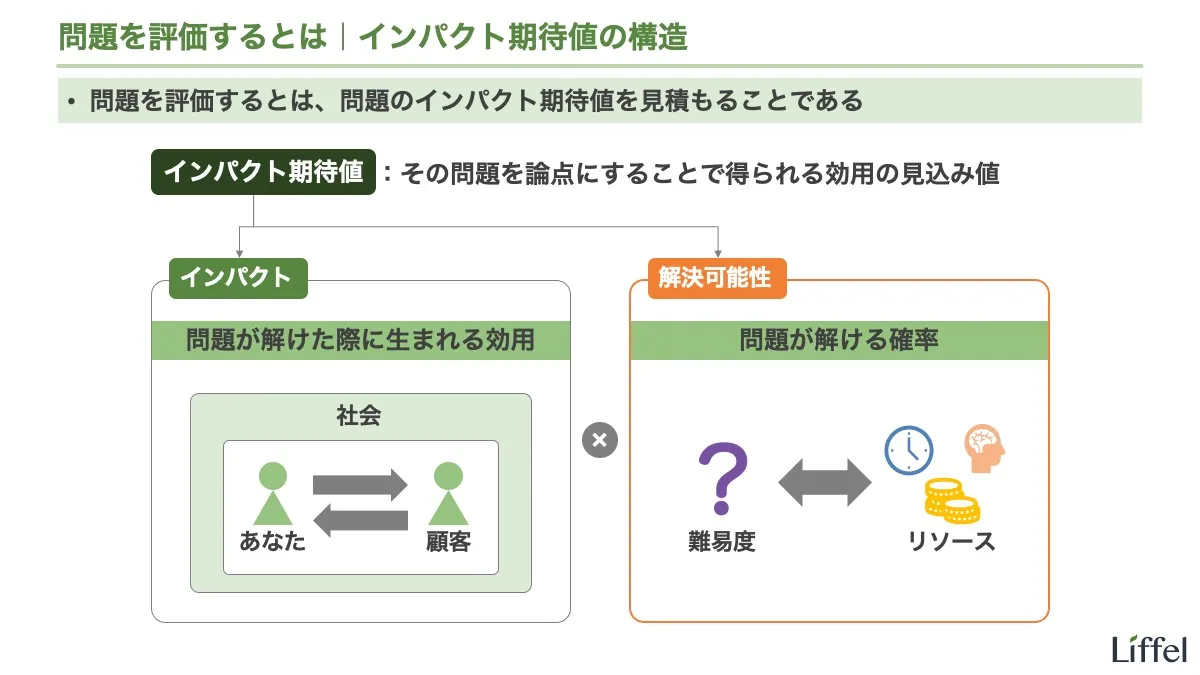
次に、解決可能性とは、問題が解ける確率のことです。これはそのままの意味ですね。
解決可能性：問題が解ける確率
スライドにあるとおり、解決可能性は問題の難易度とリソースの兼ね合いで決まります。
当然ですが、問題の難易度が上がるほど解決可能性は下がります。しかし、一般に、難易度が高い問題でないと、インパクトが大きくなりません。とにかく難易度の低い問題を選ぶというわけにはいかないのです。そこで、自分が持っているリソースと相談して、どれくらいの難易度を攻めるかを考えるわけです。
問題の難易度、リソースともに、さらに細かい視点での評価が可能です。そのあたりの話は別エントリーで行います。
インパクト期待値の論点
最後に、インパクト期待値を見積るために、何を学べばよいかを整理しておきます。まずは先ほどのスライドを確認してください。
すべきことは、大きく以下の2つです。
- 個々の要素の詳細な内容と、評価方法を理解する
- 要素に対する主観的な重み付けをする（価値観の形成）
「①個々の要素の詳細な内容と、評価方法を理解する」とは、要するに上のスライドをさらに深堀りするということです。結局のところ、細かい要素をきちんと理解しないことには、インパクトも解決可能性も評価できません。
「②要素に対する主観的な重み付けをする（価値観の形成）」は、要素の理解が終わったところで、「その中のどれを大事にするか」を考えるということです。分かりやすいのは、「知的好奇心を大事にするか、お金を大事にするか」といった話ですね。今から考えておいてください。
以上、問題を評価する大きな枠組みを紹介しました。次は、問題のインパクトを更に掘り下げていきましょう。
また、ロジカルシンキング関連のエントリーは以下のページにまとめてあります。こちらも参考にしてください。
Footnotes
-
ただし、時間の使い方が非効率になるため、高得点を狙うための最適戦略ではないでしょう。 ↩