このエントリーでは、ロジカルシンキングにおけるフレームワークとは何かを学びましょう。
フレームワークは、論点を分解する際に使える、とても便利な道具です。これなしにロジカルシンキングを行うことは不可能だと言っても過言ではありません。ここでしっかり押さえてください。
なお、「論点を分解する」ということについては、このエントリーでは詳しく説明しません。もしこの言葉にピンとこない場合は、以下のリンクから読み進めてください。
では始めましょう。
toc
フレームワークとは
早速ですが、「フレームワーク」という言葉の意味を明確にしましょう。あちこちで聞く言葉ですが、これは何を意味しているのでしょう?
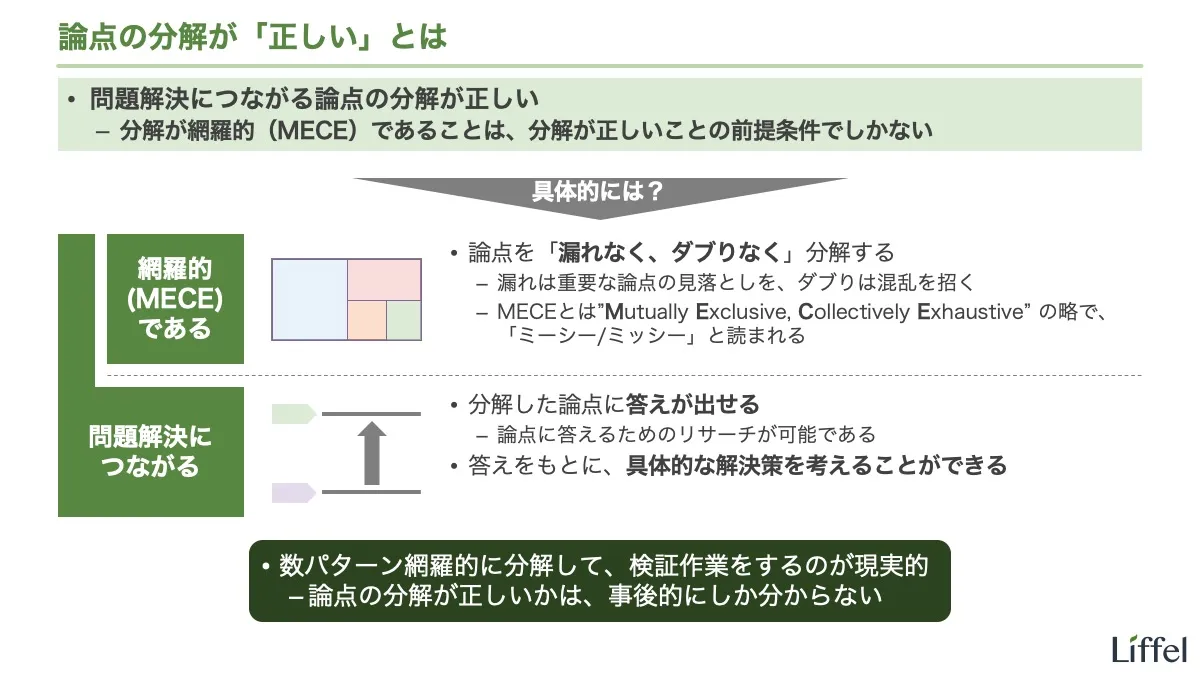
結論を先に言うと、フレームワークとは、「網羅的(MECE)なことが確定している、特定の論点の分解」のことです。つまり、フレームワークとは「ある大論点(上位の論点)」と「その大論点を分解した複数の小論点(下位の論点)」のセットのことで、その分解は網羅的になっています。数学の公式のようなものだと考えてください。
フレームワーク:網羅的(MECE)なことが確定している、特定の論点の分解
ただし、この定義は当サイト特有のものです。現在、「フレームワーク」という言葉の意味は人によってバラバラです。これ以降の説明はすべて、「フレームワーク」を上記のように定義した場合に限るので注意してください。
フレームワークの例
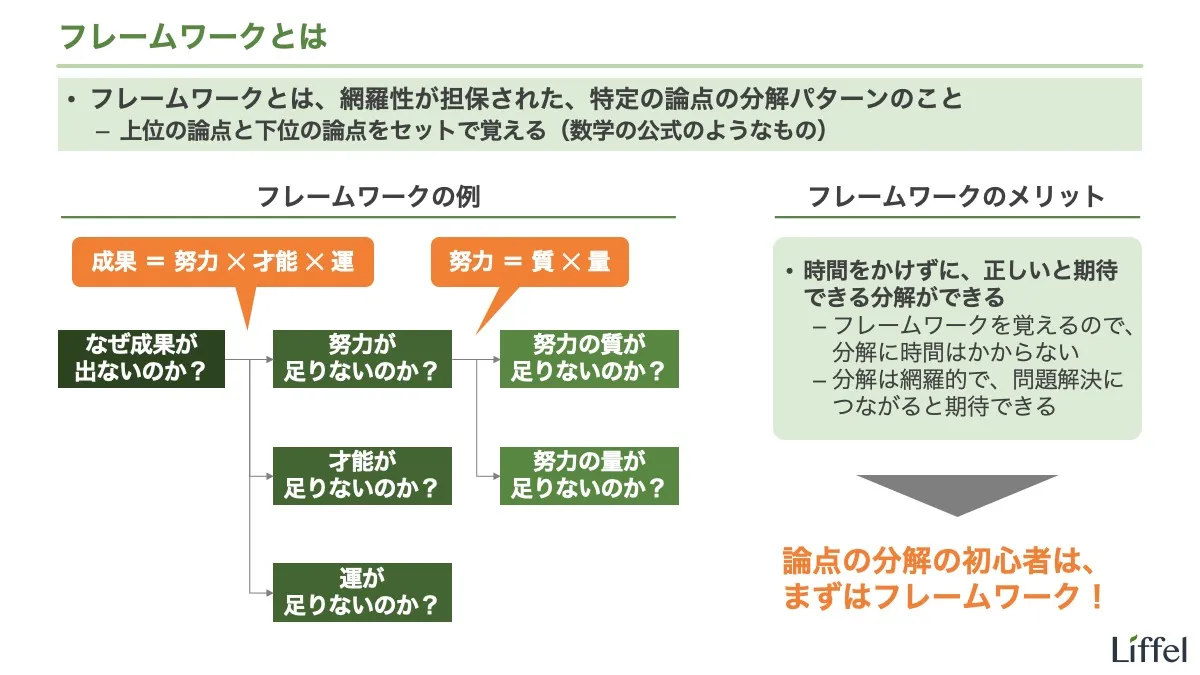
フレームワークを具体例で確認しましょう。以下のスライドを見てください。

このスライドでは、2つのフレームワークを使って論点を分解しています。「成果 = 努力 ✕ 才能 ✕ 運」と、「努力 = 質 ✕ 量」の2つです。
まず、ある特定の分野で個人として成果が出ない場合、努力と才能と運で問題を分解できます。
成果 = 努力 ✕ 才能 ✕ 運
実際に論点を分解すると、以下のようになります。
- なぜXXで成果が出ないのか?
- 努力は足りているか?
- 才能は足りているか?
- 運は足りているか?
箇条書きのインデントの位置が、大論点と小論点の関係を示しています。分解した3つの小論点に答えれば、大論点に答えが出せそうである(=ある領域における個人の成功要因は、努力、才能、運のほかには存在しない)ことを確認してください。
なお、分かりやすさのために、フレームワークそのものは「名詞の組み合わせ」の形で表現していますが、本質的に重要なのは論点(疑問文)の構造を作れることです。先述のとおり、フレームワークは論点の分解に用いるものだからです。キャッチーな名詞の形だけ覚えて、いざ論点を分解しようとするとうまくできない、といったことにならないよう注意してください。
次のフレームワークも見ておきましょう。努力は「努力の質(努力のやり方)」と「努力の量(純粋な投下時間)」に分解できます。この分解も網羅的です。
努力 = 質(努力のやり方) ✕ 量(投下時間)
このフレームワークも使えば、先ほどの論点の構造をさらに進化させられます。
- なぜXXで成果が出ないのか?
- 努力は足りているか?
- 努力の質は足りているか?(=努力のやり方は正しいか?)
- 努力の量は足りているか?(=十分な時間、努力しているか?)
- 才能は足りているか?
- 運は足りているか?
- 努力は足りているか?
このように、「ある論点に遭遇したとき、それをどのように分解するか」を暗記しておき、その論点に直面したときには、数学の公式を当てはめるように分解します。これがフレームワークを使うということです。
練習問題
習うより慣れろで、実際に先ほどのフレームワークを使ってみてください。
以下の大論点を、フレームワークを使って分解しなさい。大論点に合わせて表現を修正すること。
- なぜ成績が上がらないのか?
- なぜ部活(バスケット)でレギュラーになれないのか?
- なぜダイエットがうまくいかないのか?
今回はフレームワークに慣れることが目的なので、杓子定規に先ほどのフレームワークを当てはめてください。色々と思うところがあるかもしれませんが、それは後ほどフォローします。
- なぜ成績が上がらないのか?
- 十分な勉強をしているか?
- 勉強方法は正しいか?
- 勉強時間は足りているか?
- 才能(地頭/先天的な知的能力)は足りているか?
- 運は足りているか?
- 十分な勉強をしているか?
- なぜ部活(バスケット)でレギュラーになれないのか?
- 十分な練習をしているか?
- 練習方法は正しいか?
- 練習時間は足りているか?
- 才能(運動神経)は足りているか?
- 運は足りているか?
- 十分な練習をしているか?
- なぜダイエットがうまくいかないのか?
- 十分な努力をしているか?
- ダイエットのやり方は正しいか?
- 正しい方法を、長期にわたって実践できているか?
- 才能は足りているか?
- 運は足りているか?
- 十分な努力をしているか?
※ダイエットに関しては「努力の量」を絶対的な時間で表現するとしっくりこないので、「努力の継続」を意味する表現に変更しています。
フレームワークのメリット
論点の分解にフレームワークを使うことには、どのようなメリットがあるのでしょう?
それは、時間をかけずに正しい分解ができることです。
まず、フレームワークを使えば分解に時間はかかりません。フレームワークは覚えておくものだからです。三平方の定理を覚えておけば、直角三角形を見た瞬間に辺の長さを計算できますよね。同じように、自分の中にフレームワークを貯めこんでおけば、ある論点を見た瞬間にそれを分解できます。
そして、フレームワークを使った分解は正しい(=問題解決につながる)と期待できます。これは、以下の2つの理由からそうなります。
まず、定義により、分解が網羅的になります。分解が網羅的であることは、分解が正しくなるための前提条件です。漏れやダブりを気にせずに論点を分解できるのはありがたいですよね。
次に、長い目で見ると、網羅的なだけで問題解決に役立たないフレームワークは、誰も使わなくなるからです。そのため、生き残っているフレームワークはそれなりに便利なものだと期待できるのです。
ただし、どこかに「便利なフレームワーク認定委員会」のようなものが存在しているわけではないので、何の役にも立たないフレームワークがしぶとく生き残っているケースもそれなりに観察されます。そのあたりの話は次エントリーで説明します。
フレームワークを使えば、時間をかけずに正しい(と期待できる)分解ができる
成果を出したいなら何をするべきか?
フレームワークを使った分解は正しい(と期待できる)のであれば、その分解は問題解決につながるはずです。このことを、先ほど紹介した「成果 = 努力 ✕ 才能 ✕ 運」と「努力 = 質 ✕ 量」のフレームワークで確認してみましょう。

まず、「成果 = 努力 ✕ 才能 ✕ 運」のフレームワークから、「成果を出したいなら、努力するしかない」ということが読み取れます。才能と運を改善する解決策は、この世に存在しないからです(そもそも、才能と運の有無を検証することすら難しいですが)。この3つの要素のうち、具体的な解決策が考えられるのは努力だけです。
ここまでは当たり前の話ですが、このフレームワークは同時に「猛烈に努力しても成果が出ないことは、諦めるしかない」という、身も蓋もない話も教えてくれます。やはり、才能と運には解決策が無いからです。言い換えると、「自分が才能を持っている分野で努力するべき」ということですね。このフレームワークを持っておけば、努力教に陥ってムダな努力をせずに済みます。
そして、ここで「努力」というときに、私たちは努力の量ばかり考えがちですよね。もっとも簡単にコントロールできるのが努力の量だからです。これが、私たちが「頑張ればどうにかなる」という根性論に陥りやすい理由です。
しかし、「努力 = 質 ✕ 量」のフレームワークを持っておけば、努力には「質」という、もう1つの側面があることを忘れずに済みます。とにかく頑張ることも大事ですが、頑張り方を考えることも同じくらい大事ですよね。時間には限りがあることを考えると、質の改善のほうが重要かもしれません(量が一定水準を超えていることが大前提ですが)。
2つのフレームワークから導けるこれらのメッセージ(太字にしている部分)に、異論のある人などいないでしょう。それはつまり、このフレームワークが問題解決につながることを示しています。
このように、フレームワークを使うことのメリットは大きいです。あなたがこれまで論点を分解したことがないなら、まずは主要なフレームワークをひととおり覚えることをオススメします。
フレームワークを使って何度も論点を分解すれば、「論点を正しく分解する」ということの意味やメリットが、体感として理解できます。その感覚が身についたら、フレームワークに頼らず、自力で分解することにチャレンジすればよいでしょう。
論点の分解に慣れるまでは、フレームワークで論点を分解するのがオススメ
フレームワークの注意点
次に、フレームワークを使う際の注意点を説明します。フレームワークは便利なものですが、万能というわけではありません。限界を理解したうえで、正しく使ってください。
フレームワークの注意点は大きく以下の3点です。
- フレームワークが網羅的とは限らない
- フレームワークは小論点の重みまでは教えてくれない
- フレームワークだけでは掘り下げきれない
順に説明していきます。
注意点①:フレームワークが網羅的とは限らない
第1に、フレームワークによる分解は、分解の網羅性が100パーセント担保されているわけではありません。
先ほど、フレームワークを「網羅的(MECE)なことが確定している、特定の論点の分解」と定義しました。しかし、これはある種の誇張です。あくまで、「一般に、網羅的であると考えられている」という意味に過ぎません。
何をもって「網羅的」とするかは、主観的に決まることです。あなたが網羅的だと思っているフレームワークでも、受け手がそれに同意しないことはありえます。
たとえば、先ほど「成果 = 努力 ✕ 才能 ✕ 運」というフレームワークを紹介しました。しかし、「そもそも、努力できることが才能なのだ」というモノの見方をする人もいますよね。これだと「成果 = 才能 ✕ 運」となり、フレームワークが変化します。
どちらを採用するかは、主観的に決まることです。私としては、すべてが才能と運で決まるような世界観は受け入れがたいので、「成果 = 努力 ✕ 才能 ✕ 運」のほうが好きです。しかし、「受け入れがたい」、「好き」という言葉から分かるように、これは私の主観的な判断でしかありません。
このようなことは、多くのフレームワークに当てはまります。数学的に分解しているフレームワークを除けば1、あるフレームワークが完全に網羅的であるのかは分かりません。
ここから、新しいフレームワークを使うときには、必ず自分でチェックするべきということが言えます。そのフレームワークは網羅的なのか、問題解決に役立つのかを自分でチェックしましょう。
プレゼンのように、人を説得するときにフレームワークを使う場合は、さらなる注意が必要です。あなたが使うフレームワークに、受け手が納得するかは分かりません。使うフレームワークの正しさを、自分の言葉で説明できるようにしておきましょう。突っ込まれたときの保険になります。
あるフレームワークが使えるかは、必ず自分でチェックする
注意点②:フレームワークは小論点の重みまでは教えてくれない
第2に、フレームワークは、小論点の重みまでは教えてくれません。ここでの「重み」とは、その小論点を検証することで問題解決につながる可能性が高いかどうかです。
実際のロジカルシンキングでは、重みの大きい小論点を見定め、そこにリソースを集中投下することで素早い問題解決を目指すことが多いです。しかし、フレームワークはその視点を与えてはくれません。
例として、先ほどのダイエットの分解を見てみましょう。
- なぜダイエットがうまくいかないのか?
- 十分な努力をしているか?
- ダイエットのやり方は正しいか?
- 正しい方法を、長期にわたって実践できているか?
- 才能は足りているか?
- 運は足りているか?
- 十分な努力をしているか?
このうち、才能と運の小論点に関しては、検討する意味がありませんよね。ダイエットにおいて、才能や運の介入があるとは考えにくいからです。
まず才能ですが、勉強やスポーツにおいて、才能が重要な役割を果たすことに議論の余地はないでしょう。しかし、ダイエットではどうでしょうか。もちろん、厳密に考えれば、すべての人の「先天的な痩せる能力(痩せやすい体質かどうか)」がまったく同じということはありえないので、才能の影響はあるでしょう。しかし、飢餓状態にある人は例外なく痩せていることを考えると、すべての人には「痩せる才能」がある、つまり、才能が結果に大きな影響を与えることはないと考えて問題ないでしょう2。
運に関しても同様です。長期にわたって何度も試行を繰り返すテーマでは、運の影響は無視できます。ずっと運が良かったり、悪かったりするとは考えられないからです。その意味では、今回の練習問題で挙げた勉強、スポーツ、ダイエットは、すべて運を無視しても構いません3。
つまり、ダイエットにおいては、才能と運に関する小論点の重みはほぼゼロです。よって、重みを考慮して以下のように論点を整理するほうが問題解決(=ダイエットの成功)につながります。
- なぜダイエットがうまくいかないのか?
- ダイエットのやり方は正しいか?
- 正しい方法を、長期にわたって実践できているか?
このように、フレームワークは杓子定規な分解しか教えてくれないので、分解した小論点のどれに注力するかは、あなた自身で考える必要があります。フレームワークで分解した結果、一部の小論点に検討する意味がなさそうなら、ズバッと切り捨てる決断をしてもよいでしょう4。
フレームワークで分解した小論点のどこに注力するかは、あなた自身で考える必要がある
ただし、このような整理がうまくできるのは、事前の知識がある場合だけです。上記の論点の整理も、私にダイエットの知識があるからできることです。事前の知識が皆無である論点に取り組む場合は、とりあえずフレームワークに従っておきましょう。安全第一です。
注意点③:フレームワークだけでは掘り下げきれない
第3に、多くの場合、フレームワークだけでは掘り下げきれません。「掘り下げきれない」というのは、「検証できて、具体的な解決策が考えられるような、小さいレベルの論点に到達できない」という意味です。
引き続き、先ほどのダイエットの分解で説明します。
- なぜダイエットがうまくいかないのか?
- ダイエットのやり方は正しいか?
- 正しい方法を、長期にわたって実践できているか?
この分解は、このままでは粗すぎます。たとえば、「ダイエットのやり方」とは具体的に何のことか分かりませんよね。もう少し深いレベルまで論点を分解しないことには、論点の検証も、解決策を考えることもできません。
ここでは例として、以下のように分解してみました。
- なぜダイエットがうまくいかないのか?
- ダイエットのやり方は正しいか?
- 食事:いつ、何を、どれくらい食べているか?
- 運動:いつ、どんな運動を、どれくらい行っているか?
- 正しい方法を、長期にわたって実践できているか?
- 動機づけ:ダイエットをする理由や目的は明確になっているか?
- 計測:成果(体重)を数字で計測する仕組みがあるか? 実際に計測しているか?
- その他:そのほかに、続けるためにできる工夫はあるか?
- ダイエットのやり方は正しいか?
実際にはもっと深いレベルまで分解できますが、それはここでの主旨ではないのでやめておきます。とにかく、この分解によって、先ほどよりも具体的に考えやすくなったことを確認してください。
ここで押さえてほしいのは、私は3つめのレベルの分解にはフレームワークを使っていないということです。これらはすべて、私のこれまでのダイエットや筋トレの経験から導きました。網羅的であるかは分からないし、正しいかも分かりません(主要なポイントは押さえたつもりですが)。
このように、多くの場合、問題解決が可能なレベルまで論点を分解するには、フレームワークだけでは足りず、個別具体的な知識や経験に基づいた分解が必要になります。フレームワークというのは汎用的な公式なので、さまざまな論点に対応できる一方で、個々の論点を深いレベルまで掘り下げるには不十分なのです。
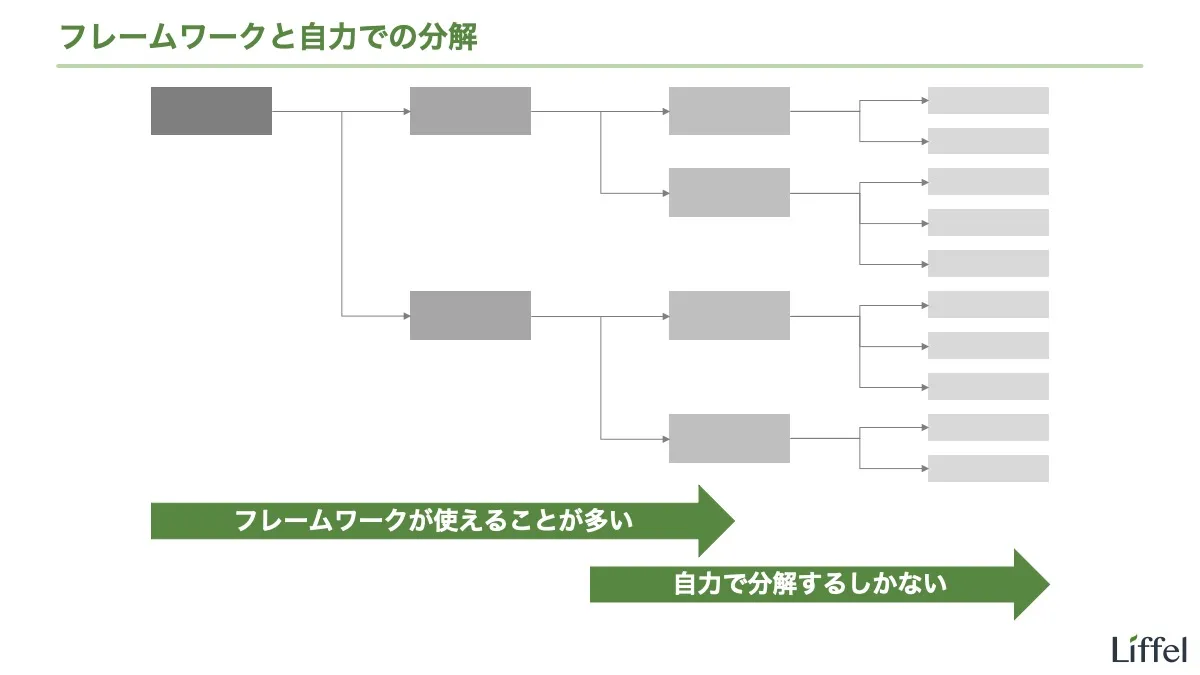
フレームワークだけで掘り下げきれない場合は、自力で頑張るしかない
ということで、最後には両方できるようになる必要があります。フレームワークだけで万事解決ということにはならないので注意してください。
それでも、まずはフレームワーク
このように、フレームワークにはいくつか注意点があります。しかし、これらは「時間をかけずに正しい分解ができる」というフレームワークのメリットを打ち消すようなものではありません。
端的に言って、フレームワークが適用できる論点で、フレームワークを使わない理由は存在しません。時間をかけずに正しい分解ができるわけですからね。もちろん、「フレームワークが適用できる」かどうかの判断が難しいのですが、間違っていたらやり直せばいいだけです。
以上、ロジカルシンキングにおけるフレームワークについて説明しました。次回は、役に立たないフレームワークの見分け方を紹介します。
また、ロジカルシンキング関連のエントリーは以下のページにまとめてあります。こちらも参考にしてください。
Footnotes
-
たとえば、「努力 = 質(努力のやり方) ✕ 量(投下時間)」のフレームワークは網羅的であると断言できます。これは「努力」を「時間」で割ってから書け戻しているだけなので、漏れがないことが数学的に明らかです。 ↩
-
特殊な病気などは例外としてあるかもしれません。 ↩
-
ただし、スポーツに関しては、監督やチームの戦術との相性などの要素を運として考えてもよいかもしれません。勉強も、受験のような一発勝負であれば、試験問題との相性という運の要素が入ってきます。 ↩
-
もちろん、そうすることによって根拠の網羅性は失われます。しかし、アカデミックな世界でないかぎり、根拠が厳密に正しいことよりも、解決策を決めて行動に移ることが優先されるのが普通です。 ↩